
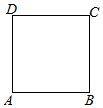
 如图,四边形ABCD是边长为2的正方形,若点P在正方形内(不含边界),且满足$\overrightarrow{PA}$$•\overrightarrow{PB}$=1
如图,四边形ABCD是边长为2的正方形,若点P在正方形内(不含边界),且满足$\overrightarrow{PA}$$•\overrightarrow{PB}$=1分析 (I)以A为原点距离平面直角坐标系,设P(x,y),求出$\overrightarrow{PA},\overrightarrow{PB}$的坐标,根据$\overrightarrow{PA}$$•\overrightarrow{PB}$=1列方程得出x,y的关系得出轨迹方程;
(2)计算|$\overrightarrow{PA}$+2$\overrightarrow{PB}$|2,使用等量代换消去平方项得出|$\overrightarrow{PA}$+2$\overrightarrow{PB}$|2关于x的函数,根据x的范围得出答案;
(3)计算|$\overrightarrow{PC}$-2$\overrightarrow{PD}$|2,消去平方项得出|$\overrightarrow{PC}$-2$\overrightarrow{PD}$|2关于x,y的函数,利用线性规划解出范围.
解答 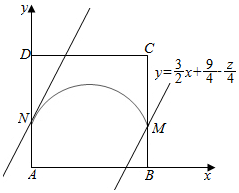 解:(I)分别以AB,AD为x轴,y轴建立平面直角坐标系,
解:(I)分别以AB,AD为x轴,y轴建立平面直角坐标系,
则A(0,0),B(2,0),设P(x,y),
则$\overrightarrow{PA}$=(-x,-y),$\overrightarrow{PB}$=(2-x,-y).
∴$\overrightarrow{PA}•\overrightarrow{PB}$=x(x-2)+y2=1,整理得:x2+y2-2x-1=0.
即动点P的轨迹方程为x2+y2-2x-1=0(0<x<2,0<y<2).
(II)$\overrightarrow{PA}+2\overrightarrow{PB}$=(4-3x,-3y),
∴($\overrightarrow{PA}+2\overrightarrow{PB}$)2=(4-3x)2+9y2=9x2+9y2-24x+16,
由(I)得x2+y2=2x+1,
∴($\overrightarrow{PA}+2\overrightarrow{PB}$)2=18x+9-24x+16=-6x+25.
∵0<x<2,
∴13<-6x+25<25,
∴$\sqrt{13}$<|$\overrightarrow{PA}+2\overrightarrow{PB}$|<5.
(III)$\overrightarrow{PC}$=(2-x,2-y),$\overrightarrow{PD}$=(-x,2-y),
$\overrightarrow{PC}-2\overrightarrow{PD}$=(x+2,y-2),
∴|$\overrightarrow{PC}$-2$\overrightarrow{PD}$|2=(x+2)2+(y-2)2=x2+y2+4x-4y+8=6x-4y+9.
令z=6x-4y+9,则y=$\frac{3}{2}x+\frac{9}{4}-\frac{z}{4}$,
由图形可知当直线y=$\frac{3}{2}x+\frac{9}{4}-\frac{z}{4}$经过点M(2,1)时,直线截距最小,即z最大,
当直线y=$\frac{3}{2}x+\frac{9}{4}-\frac{z}{4}$经过点N(0,1)时,直线截距最大,即z最小.
∴z的最大值为12-4+9=17,z的最小值为0-4+9=5.
∴|$\overrightarrow{PC}$-2$\overrightarrow{PD}$|2的取值范围是(5,17).
点评 本题考查了平面向量的数量积运算,函数的单调性与线性规划应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 0.2 | B. | 0.099 | C. | 0.198 | D. | 0.99 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
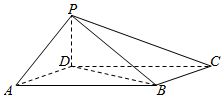 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,PD=AD=1,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,PD=AD=1,PD⊥底面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com