
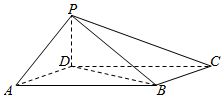
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,PD=AD=1,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,PD=AD=1,PD⊥底面ABCD.分析 (1)在△ABD中,由已知结合余弦定理可得BD⊥AD,再由线面垂直的性质可得BD⊥PD,由线面垂直的判定得到BD⊥平面PAD.从而可得PA⊥BD;
(2)利用等体积转化,代入体积公式求得棱锥D-PBC的体积.
解答 (1)证明:∵∠DAB=60°,AB=2AD,由余弦定理得BD=$\sqrt{3}$AD,
从而BD2+AD2=AB2,故BD⊥AD.
又PD⊥底面ABCD,可得BD⊥PD.
又AD∩PD=D,
∴BD⊥平面PAD.
故PA⊥BD.
(2)解:由(1)知:AD⊥BD,∴BC⊥BD,且BC=1.
在Rt△BCD中,S△BCD=$\frac{1}{2}BC•BD$=$\frac{\sqrt{3}}{2}$.
∵PD⊥底面ABCD,∴PD为三棱锥P-BCD的高,且PD=1
∴VD-PBC=VP-BCD=$\frac{1}{3}{S}_{△BCD}•PD$=$\frac{\sqrt{3}}{6}$,
∴三棱锥D-PBC的体积为$\frac{\sqrt{3}}{6}$.
点评 本题考查直线与平面垂直的判定,考查线面垂直的性质,考查了棱锥体积的求法,是中档题.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:解答题
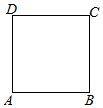 如图,四边形ABCD是边长为2的正方形,若点P在正方形内(不含边界),且满足$\overrightarrow{PA}$$•\overrightarrow{PB}$=1
如图,四边形ABCD是边长为2的正方形,若点P在正方形内(不含边界),且满足$\overrightarrow{PA}$$•\overrightarrow{PB}$=1查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨q是假命题 | B. | p∧q是真命题 | C. | p∧(¬q)是真命题 | D. | p∨(¬q)是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 36 | D. | 32 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com