
分析 (1)设z=a+bi(a,b∈R),则ω=a+$\frac{a}{{a}^{2}+{b}^{2}}$+$(b-\frac{b}{{a}^{2}+{b}^{2}})$i是实数,可得b-$\frac{b}{{a}^{2}+{b}^{2}}$=0,又z是虚数,可得b≠0,a2+b2=1.可得|z|=1,由ω=2a,-1<ω<2.即可得出z的实部的取值范围.
(2)z-2=(a-2)+bi,可得|z-2|=$\sqrt{(a-2)^{2}+{b}^{2}}$=$\sqrt{5-4a}$,利用$-\frac{1}{2}<a<1$,即可得出.
解答 解:(1)设z=a+bi(a,b∈R),则ω=z+$\frac{1}{z}$=a+bi+$\frac{1}{a+bi}$=a+$\frac{a}{{a}^{2}+{b}^{2}}$+$(b-\frac{b}{{a}^{2}+{b}^{2}})$i是实数,∴b-$\frac{b}{{a}^{2}+{b}^{2}}$=0,又z是虚数,∴b≠0,∴a2+b2=1.
∴|z|=1,∴ω=2a,∵-1<ω<2.∴-1<2a<2,解得$-\frac{1}{2}<a<1$.∴z的实部的取值范围是$(-\frac{1}{2},1)$.
(2)z-2=(a-2)+bi,∴|z-2|=$\sqrt{(a-2)^{2}+{b}^{2}}$=$\sqrt{5-4a}$,∵$-\frac{1}{2}<a<1$,∴1<5-4a<7,∴|z-2|的取值范围是$(1,\sqrt{7})$.
点评 本题考查了复数的运算法则、实部的意义、方程的解法,不等式的解法,考查了推理能力与计算能力,属于中档题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:解答题
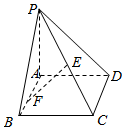 如图,在四棱锥中P-ABCD,底面ABCD为边长为$\sqrt{2}$的正方形,PA⊥BD.
如图,在四棱锥中P-ABCD,底面ABCD为边长为$\sqrt{2}$的正方形,PA⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若am2<bm2,则a<b”的逆命题是真命题 | |
| B. | 已知x∈R,则“x>2”是“x>1”的必要不充分条件 | |
| C. | 命题“p或q”为真命题,则命题“p”和命题“q”均为真命题 | |
| D. | 命题“?x∈R,使得|x|<1”的否定是:“?x∈R,都有x≤-1或x≥1” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{3}$,4) | B. | ($\frac{2}{3}$,+∞) | C. | (4,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\sqrt{3}$,$\sqrt{3}$] | B. | (-∞,$\sqrt{3}$] | C. | [-$\sqrt{3}$,+∞) | D. | (-∞,-$\sqrt{3}$]∪[$\sqrt{3}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com