
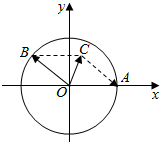
 如图,在xoy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π)
如图,在xoy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π)分析 (1)利用二倍角的余弦函数公式计算tan$\frac{θ}{2}$,代入和角的正切公式计算;
(2)利用三角形的面积公式求出Sθ=sinθ,使用辅助角公式得出Sθ+1+cosθ关于θ的函数,根据θ的范围和正弦函数的性质求出最值.
解答 解:(1)∵0<θ<π,∴0<$\frac{θ}{2}$<$\frac{π}{2}$,
∵tanθ=$\frac{\frac{4}{5}}{-\frac{3}{5}}$=-$\frac{4}{3}$,
又tanθ=$\frac{2tan\frac{θ}{2}}{1-ta{n}^{2}\frac{θ}{2}}$=-$\frac{4}{3}$.
∴tan$\frac{θ}{2}$=$\frac{1}{2}$.
∴tan($\frac{θ}{2}$+$\frac{π}{4}$)=$\frac{tan\frac{θ}{2}+tan\frac{π}{4}}{1-tan\frac{θ}{2}tan\frac{π}{4}}$=$\frac{\frac{1}{2}+1}{1-\frac{1}{2}}$=3.
(2)连结AB,则S△AOB=$\frac{1}{2}OA•OB•sinθ$=$\frac{1}{2}sinθ$,
∴Sθ=2S△AOB=sinθ,
∴Sθ+1+cosθ=1+sinθ+cosθ=1+$\sqrt{2}$sin($θ+\frac{π}{4}$).
∵0<θ<π,∴$\frac{π}{4}<$$θ+\frac{π}{4}$<$\frac{5π}{4}$.
∴当$θ+\frac{π}{4}$=$\frac{π}{2}$时,1+$\sqrt{2}$sin($θ+\frac{π}{4}$)取得最大值1+$\sqrt{2}$.
当$θ+\frac{π}{4}$=$\frac{5π}{4}$时,1+$\sqrt{2}$sin($θ+\frac{π}{4}$)取得最小值0.
∴Sθ+1+cosθ的取值范围是(0,1+$\sqrt{2}$].
点评 本题考查了三角函数的恒等变换,正弦函数的性质,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∪B={1,2,3} | B. | A=B | C. | A∩B={1,2,3} | D. | B⊆A |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 价格x | 14 | 16 | 18 | 20 | 22 |
| 需求量y | 12 | 10 | 7 | 5 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com