
 如图,在正三棱柱ABC-A1B1C1(底面为正三角形且侧棱垂直于底面的三棱柱)中,底面边长AB=3,侧棱AA1=4,AC1与A1C相交于点E,点D是BC的中点.
如图,在正三棱柱ABC-A1B1C1(底面为正三角形且侧棱垂直于底面的三棱柱)中,底面边长AB=3,侧棱AA1=4,AC1与A1C相交于点E,点D是BC的中点.分析 (Ⅰ)证明AD⊥平面BCC1B1,即可证明AD⊥C1D;
(Ⅱ)连接DE,则DE为△A1BC的中位线,得到DE∥A1B,从而得到AB∥平面ADC1;
(Ⅲ)利用三棱锥C-ABB1的体积=三棱锥A-CBB1的体积,代入体积公式进行运算.
解答 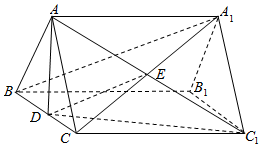 (Ⅰ)证明:∵正三棱柱ABC-A1B1C1,
(Ⅰ)证明:∵正三棱柱ABC-A1B1C1,
∴C1C⊥平面ABC,
∵AD?平面ABC,
∴C1C⊥AD,
∵点D是BC的中点,△ABC为正三角形,
∴AD⊥BC,
∵BC∩C1C=C,
∴AD⊥平面BCC1B1,
∵DC1?平面BCC1B1,
∴AD⊥C1D;
(Ⅱ)证明:连接DE,
∵四边形A1ACC1为矩形,
∴E为A1C的中点,
∵D为BD的中点,
∴ED∥A1B,
∵A1B?平面ADC1,ED?平面ADC1,
∴AB∥平面ADC1;
(Ⅲ)解:由(Ⅰ)知AD⊥平面BCC1B1,
∵AD=$\frac{3\sqrt{3}}{2}$,${S}_{△B{B}_{1}C}$=$\frac{1}{2}×3×4$=6,
∴三棱锥C-ABB1的体积=三棱锥A-CBB1的体积=$\frac{1}{3}×6×\frac{3\sqrt{3}}{2}$=3$\sqrt{3}$.
点评 本题考查证明线线垂直、线面平行的方法,求三棱锥的体积,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
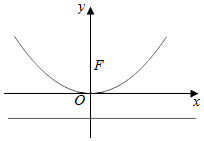 已知点F为抛物线E:x2=4y的焦点,直线l为准线,C为抛物线上的一点(C在第一象限),以点C为圆心,|CF|为半径的圆与y轴交于D,F两点,且△CDF为正三角形.
已知点F为抛物线E:x2=4y的焦点,直线l为准线,C为抛物线上的一点(C在第一象限),以点C为圆心,|CF|为半径的圆与y轴交于D,F两点,且△CDF为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
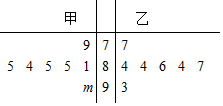 如图是七位评委为甲、乙两名比赛歌手打出的分数的茎叶图(其中m为数字0-9中的一个),甲、乙两名选手得分的平均数分别为a1,a2,若a1=a2,则m=( )
如图是七位评委为甲、乙两名比赛歌手打出的分数的茎叶图(其中m为数字0-9中的一个),甲、乙两名选手得分的平均数分别为a1,a2,若a1=a2,则m=( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费用x(万元) | 1 | 2 | 4 | 5 |
| 销售额y(万元) | 6 | 14 | 28 | 32 |
| A. | 66.2万元 | B. | 66.4万元 | C. | 66.8万元 | D. | 67.6万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∪B={1,2,3} | B. | A=B | C. | A∩B={1,2,3} | D. | B⊆A |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 价格x | 14 | 16 | 18 | 20 | 22 |
| 需求量y | 12 | 10 | 7 | 5 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com