
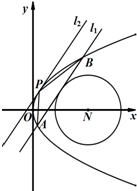
 设抛物线C:y2=2px(p>0)的焦点为F,抛物线C上点M(3,y0)满足|MF|=4.
设抛物线C:y2=2px(p>0)的焦点为F,抛物线C上点M(3,y0)满足|MF|=4.分析 (Ⅰ)利用抛物线的定义,求出p,即可求抛物线C的方程;
(Ⅱ)先表示出△PAB面积,再换元,求出△PAB面积的最小值.
解答 解:(Ⅰ)∵抛物线C上点M(3,y0)满足|MF|=4,
∴3+$\frac{p}{2}$=2,
∴p=2,…(4分)
故抛物线C的方程为y2=4x;…(5分)
(Ⅱ)设l1:x=my+n,A(x1,y1),B(x2,y2),
由l1与圆N相切得$\frac{|4-n|}{\sqrt{1+{m}^{2}}}$=3,
∴m2=$\frac{{n}^{2}-8n+7}{9}$…(7分)
由$\left\{\begin{array}{l}{x=my+n}\\{{y}^{2}=4x}\end{array}\right.$得y2-4my-4n=0
∴y1+y2=4m,y1y2=-4n
|AB|=$\sqrt{1+{m}^{2}}$|y1-y2|=4$\sqrt{1+{m}^{2}}$•$\sqrt{{m}^{2}+n}$…(10分)
不妨设l2:x=my+t,由$\left\{\begin{array}{l}x=my+t\\{y^2}=4x\end{array}\right.$得y2-4my-4t=0
∵直线l2与抛物线相切,
∴△=16m2+16t=0,
∴t=-m2,
∴l2:x=my-m2
∴l1与l2的距离为d=$\frac{|{m}^{2}+n|}{\sqrt{{m}^{2}+1}}$ …(12分)
∴S△PAB=$\frac{1}{2}$|AB|d=2$\sqrt{{m}^{2}+n}$•|m2+n|
设u=$\sqrt{{m}^{2}+n}$=$\frac{1}{3}$$\sqrt{{n}^{2}+n+7}$=$\frac{1}{3}\sqrt{(n+\frac{1}{2})^{2}+\frac{27}{4}}$≥$\frac{\sqrt{3}}{2}$
∴S△PAB=2u3$≥2×{(\frac{{\sqrt{3}}}{2})^3}=\frac{{3\sqrt{3}}}{4}$,
当n=-$\frac{1}{2}$时,△PAB面积的最小值为$\frac{3\sqrt{3}}{4}$. …(15分)
点评 本题考查抛物线的方程与定义,考查直线与抛物线的位置关系,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e=$\sqrt{2}$ | B. | e=$\frac{\sqrt{6}}{2}$ | C. | e=$\frac{\sqrt{30}}{5}$ | D. | e=$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
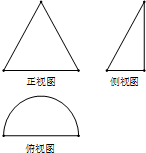 某几何体的三视图如图所示,其中正视图是腰长为2cm的等腰三角形,俯视图是半径为1cm的半圆,则该几何体的表面积是$\frac{3π}{2}$+$\sqrt{3}$cm2,体积是$\frac{\sqrt{3}}{6}$πcm3.
某几何体的三视图如图所示,其中正视图是腰长为2cm的等腰三角形,俯视图是半径为1cm的半圆,则该几何体的表面积是$\frac{3π}{2}$+$\sqrt{3}$cm2,体积是$\frac{\sqrt{3}}{6}$πcm3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com