练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    三个数72，120，168的最大公约数是 ．

     

    24

    【解析】

    试题分析：利用辗转相除法，先求出其中二个数72，120，；120，168的最大公约数，之后我们易求出三个数72，120，168的最大公约数．

    【解析】
    120=72×1+48

    72=48×1+24

    48=24×2

    ∴72，120的最大公约数是24

    168=120×1+48

    120=48×2+24

    48=24×2

    故120，168的最大公约数为24

    三个数72，120，168的最大公约数24．

    故答案为：24．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年新人教A版选修4-7 1.1什么叫优选法练习卷（解析版） 题型：填空题

    选做题（从下列二题中任选做一题，若两题全做，则只按一题计分）

    （优选法和实验设计初步选做题）某化工厂准备对一化工产品进行技术改造，决定优选加工温度，假定最佳温度在60°C到81°C之间，现用分数发进行优选，则第二个试点的温度为 ．

    （坐标系与参数方程选做题）在极坐标系中，定点A（1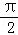，），动点B在曲线ρ=2cosθ上移动，当线段AB最短时，点B的极径为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-6 2.4一次同余方程练习卷（解析版） 题型：填空题

    （2013•永州一模）若两整数a，b除以同一个整数m，所得余数相同，则称a，b对模m同余．即当a，b，m∈z时，若=k（k∈z，k≠0），则称a、b对模m同余，用符号a=b（modm）表示．

    （1）若6=b（mod2）且0＜b＜6，则b的所有可能取值为 ；

    （2）若a=10（modm）（a＞10，m＞1），满足条件的a由小到大依次记为a1，a2…an，…，当数列{an}前m﹣1项的和为60（m﹣1）时，则m= ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-6 2.1同余练习卷（解析版） 题型：选择题

    设a、b、m为整数（m＞0），若a和b被m除得的余数相同，则称a和b对模m同余，记为a≡b（modm）．已知a=2+C+C•2+C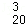•22+…+C•219，b≡a（mon10），则b的值可以是（ ）

    A.2015 B.2012 C.2008 D.2006

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-6 1.2最大公因数与最小公倍数 题型：填空题

    1248和585的最大公约数是 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-6 1.2最大公因数与最小公倍数 题型：选择题

    在对16和12求最大公约数时，整个操作如下：（16，12）→（4，12）→（4，8）→（4，4），由此可以看出12和16的最大公约数是（ ）

    A.4 B.12 C.16 D.8

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-6 1.1整除练习卷（解析版） 题型：填空题

    把七进制中的最大三位数（666）7化为三进制的数为 3．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-6 1.1整除练习卷（解析版） 题型：选择题

    将51化为二进制数得（ ）

    A.100111 B.110110 C.110011 D.110101

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.3排序不等式练习卷（解析版） 题型：解答题

    设正整数构成的数列{an}使得a10k﹣9+a10k﹣8+…+a10k≤19对一切k∈N*恒成立．记该数列若干连续项的和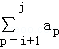为S（i，j），其中i，j∈N*，且i＜j．求证：所有S（i，j）构成的集合等于N*．

     

    查看答案和解析>>

    同步练习册答案