
(本小题满分13分)
某种产品的广告费支出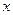 与销售额
与销售额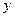 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
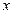 | 2 | 4 | 5 | 6 | 8 |
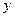 | 30 | 40 | 60 | 50 | 70 |
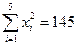
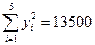
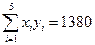 ,
,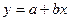 ,其中
,其中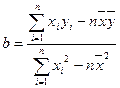 )
) 科目:高中数学 来源: 题型:解答题
(本小题满分12分)为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.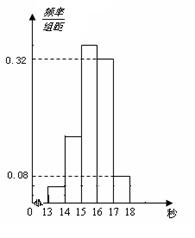
⑴将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
⑵求调查中随机抽取了多少个学生的百米成绩;
⑶若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次.记录如下:
甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
(1)画出甲、乙两位学生成绩的茎叶图,指出学生乙成绩的中位数;
(2)现要从中选派一人参加数学竞赛,从平均状况和方差的角度考虑,你认为派哪位学生参加合适?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)为了了解某年段1000名学生的百米成绩情况,随机抽取了若
干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组
[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如
图所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.
(1)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(2)求调查中随机抽取了多少个学生的百米成绩;
(3)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.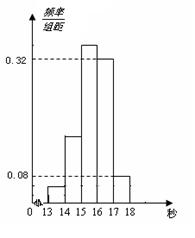
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
假设关于某设备的使用年限x和所支出的维修费用y(万元),有如下表的统计资料:
若由资料可知y对x呈线性相关关系,试求:
(1)线性回归直线方程;
(2)估计使用年限为.10年时,维修费用是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差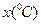 | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数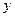 个 个 | 22 | 25 | 29 | 26 | 16 | 12 |
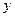 关于
关于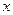 的线性回归方程
的线性回归方程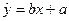 ;
;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
本小题满分12分)
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组 ,第二组
,第二组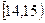 ……第五组
……第五组 ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.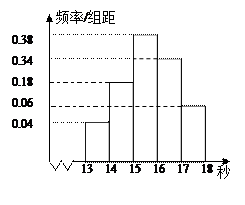
(Ⅰ)求这组数据的众数和中位数(精确到0.1);
(II)设 表示样本中两个学生的百米测
表示样本中两个学生的百米测
试成绩,已知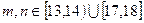
求事件“ ”的概率.
”的概率.
(Ⅲ) 根据有关规定,成绩小于16秒为达标.
如果男女生使用相同的达标标准,则男女生达标情况如下 表
表
| 性别 是否达标 | 男 | 女 | 合计 |
| 达标 | 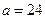 | 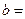 ______ ______ | _____ |
| 不达标 | 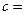 _____ _____ | 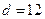 | _____ |
| 合计 | ______ | ______ | 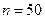 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
17.有甲乙两个班级进行数学考 试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:
试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 10[来源:学科网ZXXK] | | |
| 乙班 | | 30 | [来源:学#科#网] |
| 合计 | | | 105 |
 绩与班级有关系”。
绩与班级有关系”。查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知x与y之间的一组数据
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
 x与y线性相关,写出线性回归方程必定经过的点
x与y线性相关,写出线性回归方程必定经过的点 =0.74
=0.74 说明什么问题。
说明什么问题。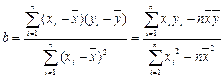
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com