
(本小题满分12分)为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.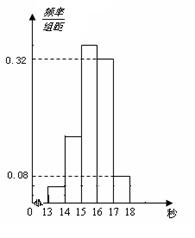
⑴将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
⑵求调查中随机抽取了多少个学生的百米成绩;
⑶若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.
(1)估计该年段学生中百米成绩在[16,17)内的人数为320人。
(2)调查中随机抽取了50个学生的百米成绩. (3)P(A )= 。
。
解析试题分析:(1)根据频率分步直方图中小正方形的面积是这组数据的频率,用长乘以宽得到面积,即为频率.
(II)根据所有的频率之和是1,列出关于x的方程,解出x的值做出样本容量的值,即调查中随机抽取了50个学生的百米成绩.
(III)本题是一个古典概型,试验发生所包含的事件是从第一、五组中随机取出两个成绩,满足条件的事件是成绩的差的绝对值大于1秒,列举出事件数,根据古典概型概率公式得到结果.
解:(1)百米成绩在[16,17)内的频率为0.32 1="0.32." 0.32
1="0.32." 0.32 1000=320
1000=320
∴估计该年段学生中百米成绩在[16,17)内的人数为320人。 ……2分
(2)设图中从左到右前3个组的频率分别为3x,8x ,19x 依题意,得 3x+8x+19x+0.32 1+0.08
1+0.08 1="1" ,∴x=0.02 ……4分
1="1" ,∴x=0.02 ……4分
设调查中随机抽取了n 个学生的百米成绩,则 ∴n=50
∴n=50
∴调查中随机抽取了50个学生的百米成绩. ……6分
(3)百米成绩在第一组的学生数有3 0.02
0.02 1
1 50=3,记他们的成绩为a,b,c
50=3,记他们的成绩为a,b,c
百米成绩在第五组的学生数有0.08 1
1 50= 4,记他们的成绩为m,n,p,q
50= 4,记他们的成绩为m,n,p,q
则从第一、五组中随机取出两个成绩包含的基本事件有
{a,b},{a,c},{a,m},{a,n},{a,p},{a,q},{b,c},{b,m},{b,n},{b,p},{b,q},{c,m},{c,n},
{c,p},{c,q},{m,n},{m,p},{m,q},{n,p},{n,q},{p,q},共21个 ……9分
设事件A为满足成绩的差的绝对值大于1秒,则事件A所包含的基本事件有{a,m},{a,n},{a,p},{a,q},{b,m},{b,n},{b,p},{b,q},{c,m},{c,n},{c,p},{c,q},共12个,……10分
所以P(A )= ……12分
……12分
考点:本试题主要考查了样本估计总体,考查古典概型的概率公式,考查频率分布直方图等知识,考查数据处理能力和分析问题、解决问题的能力。
点评:解决该试题的关键是利用直方图得到各个区间的概率值,进而结合古典概型概率公式,确定基本事件空间,和事件A发生的基本事件数,进而得到结论。


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:解答题
2013年春节前,有超过20万名广西、四川等省籍的外来务工人员选择驾乘摩托车沿321国道长途跋涉返乡过年,为防止摩托车驾驶人因长途疲劳驾驶,手脚僵硬影响驾驶操作而引发交事故,肇庆市公安交警部门在321国道沿线设立了多个长途行驶摩托车驾乘人员休息站,让过往返乡过年的摩托车驾驶人有一个停车休息的场所。交警小李在某休息站连续5天对进站休息的驾驶人员每隔50辆摩托车就进行省籍询问一次,询问结果如图所示:
(1)问交警小李对进站休息的驾驶人员的省籍询问采用的是什么抽样方法?
(2)用分层抽样的方法对被询问了省籍的驾驶人员进行抽样,若广西籍的有5名,则四川籍的应抽取几名?
(3)在上述抽出的驾驶人员中任取2名,求抽取的2名驾驶人员中四川籍人数 的分布列及其数学期望。
的分布列及其数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题12分) 某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少
某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少 的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .若备选的5个居民小区中有三个非低碳小区,两个低碳小区.
的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .若备选的5个居民小区中有三个非低碳小区,两个低碳小区.
(1)求所选的两个小区恰有一个为“非低碳小区”的概率;
(2)假定选择的“非低碳小区”为小区 ,调查显示其“低碳族”的比例为1:2,数据如图1所示,经过大力宣传,三个月后又进行一次调查,数据如图2所示,问这时小区
,调查显示其“低碳族”的比例为1:2,数据如图1所示,经过大力宣传,三个月后又进行一次调查,数据如图2所示,问这时小区 是否达到“低碳小区”的标准?
是否达到“低碳小区”的标准?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
| | 文艺节目 | 新闻节目 | 总计 |
| 20至40岁 | 40 | 10 | 50 |
| 大于40岁 | 20 | 30 | 50 |
| 总计 | 60 | 40 | 100 |
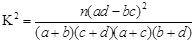
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量( 吨)与相应的生产能耗
吨)与相应的生产能耗 (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
 | 3 | 4 | 5 | 6 |
 | 2.5 | 3 | 4 | 4.5 |
 关于
关于 的线性回归方程
的线性回归方程 ;
; ,
, )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)为了调查甲、乙两个交通站的车流量,随机选取了14天,统计每天上午8∶00~12∶00间各自的车流量(单位:百辆),得如图所示的统计图,试求: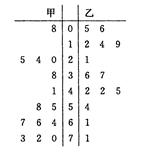
(1)甲、乙两个交通站的车流量的极差分别是多少?
(2)甲交通站的车流量在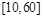 间的频率是多少?
间的频率是多少?
(3)根据该茎叶图结合所学统计知识分析甲、乙两个交通站哪个站更繁忙?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现在采用分层抽样法(层内采用不放回的简单随机抽样)从甲,乙两组中共抽取3人进行技术考核.
(1)求甲,乙两组各抽取的人数;
(2)求从甲组抽取的工人中恰有1名女工的概率;
(3)令X表示抽取的3名工人中男工人的人数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为抗击金融风暴,某系统决定对所属企业给予低息贷款的扶持,该系统制定了评分标准,并根据标准对企业进行评估,然后依据评估得分将这些企业分别定为优秀、良好、合格、不合格四个等级,并根据等级分配相应的低息贷款数额,为了更好地掌握贷款总额,该系统随机抽查了所属的部分企业.一下图表给出了有关数据(将频率看做概率)
(1)任抽一家所属企业,求抽到的企业等级是优秀或良好的概率;
(2)对照标准,企业进行了整改.整改后,如果优秀企业数量不变,不合格企业、合格企业、良好企业的数量成等差数列.要使所属企业获得贷款的平均值(即数学期望)不低于410万元,那么整改后不合格企业占企业总数百分比的最大值是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
某种产品的广告费支出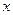 与销售额
与销售额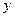 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
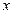 | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
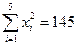
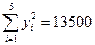
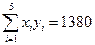 ,
,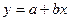 ,其中
,其中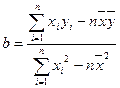 )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com