
| A. | $[kπ-\frac{3π}{8},kπ+\frac{π}{8}],(k∈Z)$ | B. | $[kπ-\frac{π}{8},kπ+\frac{3π}{8}],(k∈Z)$ | ||
| C. | $[2kπ-\frac{3π}{4},2kπ+\frac{π}{4}],(k∈Z)$ | D. | $[2kπ-\frac{π}{4},2kπ+\frac{3π}{4}],(k∈Z)$ |
分析 依题意,f(0)=f($\frac{π}{4}$),可求得m=-1,利用辅助角公式可得f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),从而可求得f(x)的单调递增区间.
解答 解:函数$f(x)=|{\begin{array}{l}{2sinx}&m\\{cos2x}&{cosx}\end{array}}|$=sin2x-mcos2x的图象关于直线x=$\frac{π}{8}$对称,
∴f(0)=f($\frac{π}{4}$),即-m=1,
∴m=-1,
∴f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),
由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{4}$≤$\frac{π}{2}$+2kπ,k∈Z得:
kπ-$\frac{3π}{8}$≤x≤$\frac{π}{8}$+kπ,k∈Z.
故选:A.
点评 本题考查正弦函数的单调性,考查y=Asin(ωx+φ)的图象与性质,考查分析与转化的能力,属于中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
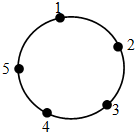 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点,若它停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这个点开始跳,则经2015次跳后停在的点对应的数为3.
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点,若它停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这个点开始跳,则经2015次跳后停在的点对应的数为3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{4}{3}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
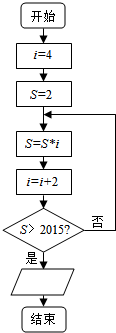
| A. | 输出i-2 | B. | 输出i-1 | C. | 输出i | D. | 输出i+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com