
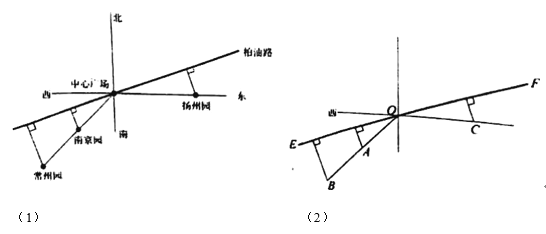
ЎѕМвДїЎїЅЛХКЎФ°І©»бУРТ»ЦРРД№гіЎЈ¬ДПѕ©Ф°Ј¬іЈЦЭФ°¶јФЪЦРРД№гіЎµДДПЖ«Оч45Ўг·ЅПтЙПЈ¬µЅЦРРД№гіЎµДѕаАл·Ц±рОЄ![]() kmЈ¬
kmЈ¬![]() kmЈ»СпЦЭФ°ФЪЦРРД№гіЎµДХэ¶«·ЅПтЈ¬µЅЦРРД№гіЎµДѕаАлОЄ
kmЈ»СпЦЭФ°ФЪЦРРД№гіЎµДХэ¶«·ЅПтЈ¬µЅЦРРД№гіЎµДѕаАлОЄ![]() kmЈ®№ж»®ЅЁЙиТ»Мх±КЦ±µД°ШУНВ·ґ©№эЦРРД№гіЎЈ¬ЗТЅ«ДПѕ©Ф°Ј¬іЈЦЭФ°Ј¬СпЦЭФ°µЅ°ШУНВ·µДЧо¶МВ·ѕ¶ЖМЙиіЙ¶мВСКЇВ·ЈЁИзНј(1)Ўў(2)Ј©Ј®ТСЦЄЖМЙиГї¶О¶мВСКЇВ·µД·СУГЈЁНтФЄЈ©УлЖді¤¶ИµДЖЅ·ЅіЙХэ±ИЈ¬±ИАэПµКэОЄ2Ј®Йи°ШУНВ·УлХэ¶«·ЅПтµДјРЅЗЈ¬јґНј(2)ЦРЎПCOFОЄ
kmЈ®№ж»®ЅЁЙиТ»Мх±КЦ±µД°ШУНВ·ґ©№эЦРРД№гіЎЈ¬ЗТЅ«ДПѕ©Ф°Ј¬іЈЦЭФ°Ј¬СпЦЭФ°µЅ°ШУНВ·µДЧо¶МВ·ѕ¶ЖМЙиіЙ¶мВСКЇВ·ЈЁИзНј(1)Ўў(2)Ј©Ј®ТСЦЄЖМЙиГї¶О¶мВСКЇВ·µД·СУГЈЁНтФЄЈ©УлЖді¤¶ИµДЖЅ·ЅіЙХэ±ИЈ¬±ИАэПµКэОЄ2Ј®Йи°ШУНВ·УлХэ¶«·ЅПтµДјРЅЗЈ¬јґНј(2)ЦРЎПCOFОЄ![]() ЈЁ
ЈЁ![]() (0Ј¬
(0Ј¬![]() )Ј©Ј¬ЖМЙиИэ¶О¶мВСКЇВ·µДЧЬ·СУГОЄyЈЁНтФЄЈ©Ј®
)Ј©Ј¬ЖМЙиИэ¶О¶мВСКЇВ·µДЧЬ·СУГОЄyЈЁНтФЄЈ©Ј®
ЈЁ1Ј©ЗуДПѕ©Ф°µЅ°ШУНВ·µДЧо¶МѕаАл![]() №ШУЪ
№ШУЪ![]() µД±нґпКЅЈ»
µД±нґпКЅЈ»
ЈЁ2Ј©ЗуyµДЧоРЎЦµј°ґЛК±tan![]() µДЦµЈ®
µДЦµЈ®
Ўѕґр°ёЎїЈЁ1Ј©![]() Ј»ЈЁ2Ј©ЖМЙиИэМх¶мВСКЇВ·µДЧЬ·СУГОЄ(
Ј»ЈЁ2Ј©ЖМЙиИэМх¶мВСКЇВ·µДЧЬ·СУГОЄ(![]() )НтФЄЈ¬ґЛК±
)НтФЄЈ¬ґЛК±![]() µДЦµОЄ
µДЦµОЄ![]() .
.
ЎѕЅвОцЎї
ЈЁ1Ј©УЙЎПCOF=¦ИЈ¬ДПѕ©Ф°ФЪЦРРД№гіЎµДДПЖ«Оч45Ўг·ЅПтЙПЈ¬ЗТµЅЦРРД№гіЎµДѕаАлОЄ![]() Ј¬ЗуіцЎПAOE=
Ј¬ЗуіцЎПAOE=![]() Ј¬УЙґЛДЬЗуіцДПѕ©Ф°µЅ°ШУНВ·µДЧо¶МѕаАлd1№ШУЪ¦ИµД±нґпКЅЈ®
Ј¬УЙґЛДЬЗуіцДПѕ©Ф°µЅ°ШУНВ·µДЧо¶МѕаАлd1№ШУЪ¦ИµД±нґпКЅЈ®
ЈЁ2Ј©·Ц±рЙиµгBЈ¬CµЅЦ±ПЯEFµДѕаАлОЄd2Ј¬d3Ј¬Фт![]() Ј¬Зуіцy=2[ЈЁ
Ј¬Зуіцy=2[ЈЁ![]() Ј©2+ЈЁ2
Ј©2+ЈЁ2![]() Ј©2+ЈЁ
Ј©2+ЈЁ![]() Ј©2]=20©Ѓ10
Ј©2]=20©Ѓ10![]() sinЈЁ2
sinЈЁ2![]() Ј©Ј¬¦ИЎКЈЁ0Ј¬
Ј©Ј¬¦ИЎКЈЁ0Ј¬![]() Ј©Ј¬УЙґЛДЬЗуіцЖМЙиИэМх¶мВСКЇВ·µДЧЬ·СУГyµДЧоРЎЦµј°ґЛК±tan¦ИµДЦµЈ®
Ј©Ј¬УЙґЛДЬЗуіцЖМЙиИэМх¶мВСКЇВ·µДЧЬ·СУГyµДЧоРЎЦµј°ґЛК±tan¦ИµДЦµЈ®
ЈЁ1Ј©ЎЯЎПCOF=¦ИЈ¬
ДПѕ©Ф°ФЪЦРРД№гіЎµДДПЖ«Оч45Ўг·ЅПтЙПЈ¬ЗТµЅЦРРД№гіЎµДѕаАлОЄ![]()
ЎаЎПAOE=![]() Ј¬
Ј¬
ЎаДПѕ©Ф°µЅ°ШУНВ·µДЧо¶МѕаАлd1№ШУЪ¦ИµД±нґпКЅОЄd1=![]() sinЈЁ
sinЈЁ![]() ©Ѓ¦ИЈ©Ј®
©Ѓ¦ИЈ©Ј®
ЈЁ2Ј©·Ц±рЙиµгBЈ¬CµЅЦ±ПЯEFµДѕаАлОЄd2Ј¬d3Ј®
УЙЈЁ1Ј©ЦЄЈє![]() Ј¬
Ј¬
Ўаy=2[ЈЁ![]() Ј©2+ЈЁ2
Ј©2+ЈЁ2![]() Ј©2+ЈЁ
Ј©2+ЈЁ![]() Ј©2]
Ј©2]
=20[![]() +
+![]() ]
]
=20©Ѓ10ЈЁsin2¦И+cos2¦ИЈ©
=20©Ѓ10![]() sinЈЁ2
sinЈЁ2![]() Ј©Ј¬¦ИЎКЈЁ0Ј¬
Ј©Ј¬¦ИЎКЈЁ0Ј¬![]() Ј©Ј¬
Ј©Ј¬
ЎЯ![]() Ўа
Ўа![]() Ј¬
Ј¬
Ўаµ±2![]() =
=![]() К±Ј¬ymin=20©Ѓ10
К±Ј¬ymin=20©Ѓ10![]() ЈЁНтФЄЈ©
ЈЁНтФЄЈ©
ґЛК±2![]() Ј¬
Ј¬
Ўаtan2¦И=![]() =1Ј¬
=1Ј¬
ЅвµГЈєtan![]() Ј¬
Ј¬
ЎаЖМЙиИэМх¶мВСКЇВ·µДЧЬ·СУГОЄЈЁ20©Ѓ10![]() Ј©НтФЄЈ¬ґЛК±tan¦ИµДЦµОЄ
Ј©НтФЄЈ¬ґЛК±tan¦ИµДЦµОЄ![]() Ј®
Ј®


 ГыРЈБ·їјѕнЖЪД©іеґМѕнПµБРґр°ё
ГыРЈБ·їјѕнЖЪД©іеґМѕнПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄНЦФІ![]() µДБЅЅ№µг·Ц±рОЄ
µДБЅЅ№µг·Ц±рОЄ![]() Ј¬Жд¶М°лЦбі¤ОЄ
Ј¬Жд¶М°лЦбі¤ОЄ![]() .
.
ЈЁ1Ј©ЗуНЦФІ![]() µД·ЅіМЈ»
µД·ЅіМЈ»
ЈЁ2Ј©ЙиІ»ѕ№эµг![]() µДЦ±ПЯ
µДЦ±ПЯ![]() УлНЦФІ
УлНЦФІ![]() ПаЅ»УЪБЅµг
ПаЅ»УЪБЅµг![]() .ИфЦ±ПЯ
.ИфЦ±ПЯ![]() Ул
Ул![]() µДР±ВКЦ®єНОЄ
µДР±ВКЦ®єНОЄ![]() Ј¬ЗуКµКэ
Ј¬ЗуКµКэ![]() µДЦµ.
µДЦµ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїУРПВБРЛµ·ЁЈє
ўЩФЪІРІоНјЦРЈ¬ІРІоµг±ИЅПѕщФИµШВдФЪЛ®ЖЅµДґшЧґЗшУтДЪЈ¬ЛµГчСЎУГµДДЈРН±ИЅПєПККЈ»
ўЪУГПа№ШЦёКэR2АґїМ»»Ш№йµДР§№ыЈ¬R2ЦµФЅґуЈ¬ЛµГчДЈРНµДДвєПР§№ыФЅєГЈ»
ўЫ±ИЅПБЅёцДЈРНµДДвєПР§№ыЈ¬їЙТФ±ИЅПІРІоЖЅ·ЅєНµДґуРЎЈ¬ІРІоЖЅ·ЅєНФЅРЎµДДЈРНЈ¬ДвєПР§№ыФЅєГЈ®
ўЬФЪСРѕїЖшОВєНИИІиПъКЫ±КэµД№ШПµК±Ј¬ИфЗуµГПа№ШЦёКэR2ЎЦ0.85Ј¬Фт±нГчЖшОВЅвКНБЛ15ЈҐµДИИІиПъКЫ±Кэ±д»Ї.
ЖдЦРХэИ·ГьМвµДёцКэКЗ(ЎЎЎЎ)
A. 1 B. 2 C. 3 D. 4
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїНіјЖС§ЦРЈ¬ѕіЈУГ»·±ИЎўН¬±ИАґЅшРРКэѕЭ±ИЅПЈ¬»·±ИКЗЦё±ѕЖЪНіјЖКэѕЭУлЙПЖЪ±ИЅПЈ¬Из![]() Дк
Дк![]() ФВУл
ФВУл![]() Дк
Дк![]() ФВПа±ИЈ¬Н¬±ИКЗЦё±ѕЖЪКэѕЭУлАъК·Н¬К±ЖЪ±ИЅПЈ¬Из
ФВПа±ИЈ¬Н¬±ИКЗЦё±ѕЖЪКэѕЭУлАъК·Н¬К±ЖЪ±ИЅПЈ¬Из![]() Дк
Дк![]() ФВУл
ФВУл![]() Дк
Дк![]() ФВПа±И.
ФВПа±И.
»·±ИФці¤ВК![]() ЈЁ±ѕЖЪКэ
ЈЁ±ѕЖЪКэ![]() ЙПЖЪКэЈ©
ЙПЖЪКэЈ©![]() ЙПЖЪКэ
ЙПЖЪКэ![]() Ј¬
Ј¬
Н¬±ИФці¤ВК![]() ЈЁ±ѕЖЪКэ
ЈЁ±ѕЖЪКэ![]() Н¬ЖЪКэЈ©
Н¬ЖЪКэЈ©![]() Н¬ЖЪКэ
Н¬ЖЪКэ![]() .
.
ПВ±нКЗДіµШЗшЅь![]() ёцФВАґµДПы·СХЯРЕРДЦёКэµДНіјЖКэѕЭЈє
ёцФВАґµДПы·СХЯРЕРДЦёКэµДНіјЖКэѕЭЈє
РтєЕ |
|
|
|
|
|
|
|
|
К±јд |
|
|
|
|
|
|
|
|
Пы·СХЯРЕРДЦёКэ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2017Дк
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]() ЗуёГµШЗш
ЗуёГµШЗш![]() Дк
Дк![]() ФВПы·СХЯРЕРДЦёКэµДН¬±ИФці¤ВКЈЁ°Щ·Ц±ИРОКЅПВ±ЈБфХыКэЈ©Ј»
ФВПы·СХЯРЕРДЦёКэµДН¬±ИФці¤ВКЈЁ°Щ·Ц±ИРОКЅПВ±ЈБфХыКэЈ©Ј»
![]() іэ
іэ![]() Дк
Дк![]() ФВТФНвЈ¬ёГµШЗшПы·СХЯРЕРДЦёКэФВ»·±ИФці¤ВКОЄёєКэµДУРјёёцФВЈї
ФВТФНвЈ¬ёГµШЗшПы·СХЯРЕРДЦёКэФВ»·±ИФці¤ВКОЄёєКэµДУРјёёцФВЈї
![]() УЙТФЙПКэѕЭїЙЕР¶ПЈ¬РтєЕ
УЙТФЙПКэѕЭїЙЕР¶ПЈ¬РтєЕ![]() УлёГµШЗшПы·СХЯРЕРДЦёКэ
УлёГµШЗшПы·СХЯРЕРДЦёКэ![]() ѕЯУРПЯРФПа№Ш№ШПµЈ¬Рґіц
ѕЯУРПЯРФПа№Ш№ШПµЈ¬Рґіц![]() №ШУЪ
№ШУЪ![]() µДПЯРФ»Ш№й·ЅіМ
µДПЯРФ»Ш№й·ЅіМ![]() ЈЁ
ЈЁ![]() Ј¬
Ј¬![]() ±ЈБф
±ЈБф![]() О»РЎКэЈ©Ј¬ІўТАґЛФ¤ІвёГµШЗш
О»РЎКэЈ©Ј¬ІўТАґЛФ¤ІвёГµШЗш![]() Дк
Дк![]() ФВµДПы·СХЯРЕРДЦёКэЈЁЅб№ы±ЈБф
ФВµДПы·СХЯРЕРДЦёКэЈЁЅб№ы±ЈБф![]() О»РЎКэЈ¬ІОїјКэѕЭУ빫ʽЈє
О»РЎКэЈ¬ІОїјКэѕЭУ빫ʽЈє![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬ Ј©
Ј©
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ТСЦЄХэ·ЅМе![]() Ј¬
Ј¬![]() ОЄАв
ОЄАв![]() µДЦРµгЈ¬
µДЦРµгЈ¬![]() ОЄАв
ОЄАв![]() µД¶ЇµгЈ¬ЙиЦ±ПЯ
µД¶ЇµгЈ¬ЙиЦ±ПЯ![]() ОЄЖЅГж
ОЄЖЅГж![]() УлЖЅГж
УлЖЅГж![]() µДЅ»ПЯЈ¬Ц±ПЯ
µДЅ»ПЯЈ¬Ц±ПЯ![]() ОЄЖЅГж
ОЄЖЅГж![]() УлЖЅГж
УлЖЅГж![]() µДЅ»ПЯЈ¬ПВБРЅбВЫЦРґнОуµДКЗ( )
µДЅ»ПЯЈ¬ПВБРЅбВЫЦРґнОуµДКЗ( )

A.![]() ЖЅГж
ЖЅГж![]() B.ЖЅГж
B.ЖЅГж![]() УлЖЅГж
УлЖЅГж![]() І»ґ№Ц±
І»ґ№Ц±
C.ЖЅГж![]() УлЖЅГж
УлЖЅГж![]() їЙДЬЖЅРРD.Ц±ПЯ
їЙДЬЖЅРРD.Ц±ПЯ![]() УлЦ±ПЯ
УлЦ±ПЯ![]() їЙДЬІ»ЖЅРР
їЙДЬІ»ЖЅРР
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
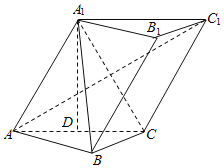
ЎѕМвДїЎїИзНјЈ¬ИэАвЦщABC-A1B1C1ЦРЈ¬ЎПBCA=90ЎгЈ¬AC=BC=AA1=A1C=2Ј¬ЖЅГжACC1A1ЎНЖЅГжABC.ПЦТФ±ЯACµДЦРµгDОЄЧш±кФµгЈ¬ЖЅГжABCДЪґ№Ц±УЪACµДЦ±ПЯОЄ![]() ЦбЈ¬Ц±ПЯACОЄ
ЦбЈ¬Ц±ПЯACОЄ![]() ЦбЈ¬Ц±ПЯDA1ОЄ
ЦбЈ¬Ц±ПЯDA1ОЄ![]() ЦбЅЁБўїХјдЦ±ЅЗЧш±кПµЈ¬ЅвѕцТФПВОКМв:
ЦбЅЁБўїХјдЦ±ЅЗЧш±кПµЈ¬ЅвѕцТФПВОКМв:
ЈЁ1Ј©ЗуТмГжЦ±ПЯABУлA1CЛщіЙЅЗµДУаПТЦµЈ»
ЈЁ2Ј©ЗуЦ±ПЯABУлЖЅГжA1BCЛщіЙЅЗµДХэПТЦµ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() Ј¬Иф¶ФИОТвµД
Ј¬Иф¶ФИОТвµД![]() ЗТ
ЗТ![]() Ј¬¶јУР
Ј¬¶јУР![]() Ј¬ФтКµКэ
Ј¬ФтКµКэ![]() µДИЎЦµ·¶О§КЗ( )
µДИЎЦµ·¶О§КЗ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїPM2.5КЗЦёґуЖшЦРЦ±ѕ¶РЎУЪ»тµИУЪ2.5ОўГЧµДїЕБЈОпЈ¬ТІіЖОЄїЙИл·ОїЕБЈОпЈ¬Т»°гЗйїцПВPM2.5µДЕЁ¶ИФЅґуЈ¬ґуЖш»·ѕіЦКБїФЅІо.УТ±ЯµДѕҐТ¶Нј±нКѕµДКЗіЙ¶јКРЗшјЧТТБЅёцјаІвХѕДі10ИХДЪГїМмµДPM2.5ЕЁ¶И¶БКэ(µҐО»Јє![]() )Ј¬ФтПВБРЛµ·ЁХэИ·µДКЗ( )
)Ј¬ФтПВБРЛµ·ЁХэИ·µДКЗ( )

A.Хв10ИХДЪјЧЎўТТјаІвХѕ¶БКэµДј«ІоПаµИ
B.Хв10ИХДЪјЧЎўТТјаІвХѕ¶БКэµДЦРО»КэЦРЈ¬ТТµДЅПґу
C.Хв10ИХДЪТТјаІвХѕ¶БКэµДЦЪКэУлЦРО»КэПаµИ
D.Хв10ИХДЪјЧЎўТТјаІвХѕ¶БКэµДЖЅѕщКэПаµИ
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬![]() КЗ°лФІ
КЗ°лФІ![]() µДЦ±ѕ¶Ј¬
µДЦ±ѕ¶Ј¬![]() Ј¬
Ј¬![]() ОЄФІЦЬЙПТ»µгЈ¬
ОЄФІЦЬЙПТ»µгЈ¬![]() ЖЅГж
ЖЅГж![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() .
.

ЈЁ1Ј©ЗуЦ¤ЈєЖЅГж![]() ЖЅГж
ЖЅГж![]() Ј»
Ј»
ЈЁ2Ј©ФЪПЯ¶О![]() ЙПКЗ·сґжФЪµг
ЙПКЗ·сґжФЪµг![]() Ј¬ЗТК№µГ
Ј¬ЗТК№µГ![]() ЖЅГж
ЖЅГж![]() ЈїИфґжФЪЈ¬Зуіцµг
ЈїИфґжФЪЈ¬Зуіцµг![]() µДО»ЦГЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙ.
µДО»ЦГЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙ.
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com