
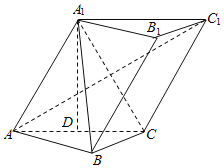
【题目】如图,三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=A1C=2,平面ACC1A1⊥平面ABC.现以边AC的中点D为坐标原点,平面ABC内垂直于AC的直线为![]() 轴,直线AC为
轴,直线AC为![]() 轴,直线DA1为
轴,直线DA1为![]() 轴建立空间直角坐标系,解决以下问题:
轴建立空间直角坐标系,解决以下问题:
(1)求异面直线AB与A1C所成角的余弦值;
(2)求直线AB与平面A1BC所成角的正弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)以边AC的中点D为坐标原点,平面ABC内垂直于AC的直线为x轴,直线AC为y轴,直线DA1为z轴建立空间直角坐标系,利用向量法能求出异面直线AB与A1C所成角的余弦值.
(2)求出平面A1BC的法向量,利用向量法能求出直线AB与平面A1BC所成角的正弦值.
(1)三棱柱ABC﹣A1B1C1中,∠BCA=90°,AC=BC=AA1=A1C=2,平面ACC1A1⊥平面ABC.
以边AC的中点D为坐标原点,
平面ABC内垂直于AC的直线为x轴,
直线AC为y轴,直线DA1为z轴建立空间直角坐标系,
根据题中空间直角坐标系可知:
A(0,﹣1,0),C(0,1,0),B(2,1,0),A1(0,0,![]() ),
),
∴![]() =(2,2,0),
=(2,2,0),![]() =(0,1,﹣
=(0,1,﹣![]() ),
),
∴cos<![]() >=
>=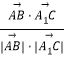 =
=![]() =
=![]() ,
,
设异面直线AB与A1C的所成角为α,则![]() ,
,
∴异面直线AB与A1C所成角的余弦值为![]() .
.
(2)由(1)得:![]() =(2,1,﹣
=(2,1,﹣![]() ),
),![]() =(﹣2,0,0),
=(﹣2,0,0),
设平面A1BC的法向量为![]() =(x,y,z),
=(x,y,z),
∴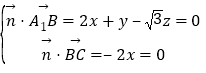 ,取z=1,则
,取z=1,则![]() =(0,
=(0,![]() ),
),
∴cos<![]() ,
,![]() >=
>=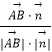 =
=![]() =
=![]() .
.
设直线AB与平面A1BC所成角为β,β∈(0,![]() ],
],
则sinβ=|cos<![]() ,
,![]() >|=
>|=![]() .
.
故直线AB与平面A1BC所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
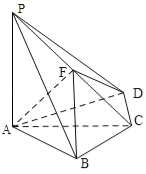
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=![]() ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.
(1)求PA的长;
(2)求二面角B﹣AF﹣D的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 。
。
Ⅰ.求函数![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
Ⅱ.当![]() 时,方程
时,方程![]() 恰有两个不同的实数根,求实数
恰有两个不同的实数根,求实数![]() 的取值范围;
的取值范围;
Ⅲ.将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后所得函数
个单位后所得函数![]() 的图象关于原点中心对称,求
的图象关于原点中心对称,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
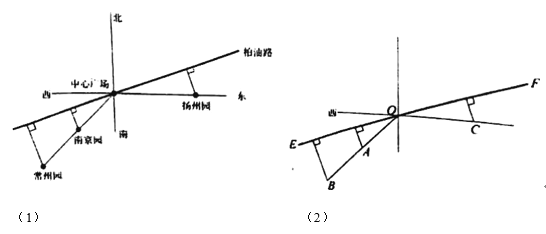
【题目】江苏省园博会有一中心广场,南京园,常州园都在中心广场的南偏西45°方向上,到中心广场的距离分别为![]() km,
km,![]() km;扬州园在中心广场的正东方向,到中心广场的距离为
km;扬州园在中心广场的正东方向,到中心广场的距离为![]() km.规划建设一条笔直的柏油路穿过中心广场,且将南京园,常州园,扬州园到柏油路的最短路径铺设成鹅卵石路(如图(1)、(2)).已知铺设每段鹅卵石路的费用(万元)与其长度的平方成正比,比例系数为2.设柏油路与正东方向的夹角,即图(2)中∠COF为
km.规划建设一条笔直的柏油路穿过中心广场,且将南京园,常州园,扬州园到柏油路的最短路径铺设成鹅卵石路(如图(1)、(2)).已知铺设每段鹅卵石路的费用(万元)与其长度的平方成正比,比例系数为2.设柏油路与正东方向的夹角,即图(2)中∠COF为![]() (
(![]() (0,
(0,![]() )),铺设三段鹅卵石路的总费用为y(万元).
)),铺设三段鹅卵石路的总费用为y(万元).
(1)求南京园到柏油路的最短距离![]() 关于
关于![]() 的表达式;
的表达式;
(2)求y的最小值及此时tan![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是

A. 56 B. 60 C. 120 D. 140
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com