
【题目】已知函数![]() 的部分图象如图所示.
的部分图象如图所示.
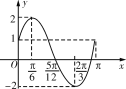
(1)求函数的解析式;
(2)设![]() ,且方程
,且方程![]() 有两个不同的实数根,求实数m的取值范围和这两个根的和.
有两个不同的实数根,求实数m的取值范围和这两个根的和.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ,当
,当![]() 时,两根和为
时,两根和为![]() ,当
,当![]() 时,两根和为
时,两根和为![]() .
.
【解析】
试题分析:(1)由函数图象的顶点坐标可知![]() ,由图象过
,由图象过![]() ,可求得
,可求得![]() 的值,由五点法可求得
的值,由五点法可求得![]() 的值,由此得到了函数的解析式;(2)在同一坐标系下画出
的值,由此得到了函数的解析式;(2)在同一坐标系下画出![]() 和直线
和直线![]() 的图象,结合正弦函数的图象的特征,数形结合求得实数
的图象,结合正弦函数的图象的特征,数形结合求得实数![]() 的取值范围和这两个根的和.
的取值范围和这两个根的和.
试题解析:(1)显然![]() ,又图象过(0,1)点,∴
,又图象过(0,1)点,∴![]() f(0)=1,
f(0)=1,
∴sinφ=![]() ,∵|φ|<
,∵|φ|<![]() ,∴φ=
,∴φ=![]() ;
;
由图象结合“五点法”可知,![]() 对应函数y=sinx图象的点(2π,0),
对应函数y=sinx图象的点(2π,0),
∴ω·![]() +
+![]() =2π,得ω=2.
=2π,得ω=2.
所以所求的函数的解析式为:f(x)=2sin![]() .
.
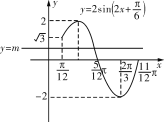
(2)如图所示,在同一坐标系中画出![]() 和y=m(m∈R)的图象,
和y=m(m∈R)的图象,
由图可知,当-2<m<0或![]() <m<2时,直线y=m与曲线有两个不同的交点,即原方程有两个不同的实数根. ∴m的取值范围为:-2<m<0或
<m<2时,直线y=m与曲线有两个不同的交点,即原方程有两个不同的实数根. ∴m的取值范围为:-2<m<0或![]() <m<2
<m<2
当-2<m<0时,两根和为![]() ;当
;当![]() <m<2时,两根和为
<m<2时,两根和为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知圆C经过点![]() ,
,![]() ,且圆心在直线
,且圆心在直线![]() 上
上
(1)求圆C的方程.
(2)过点![]() 的直线与圆C交于A,B两点,问:在直线
的直线与圆C交于A,B两点,问:在直线![]() 上是否存在定点N,使得
上是否存在定点N,使得![]() (
(![]() ,
,![]() 分别为直线AN,BN的斜率)恒成立?若存在,请求出点N的坐标;若不存在,请说明理由.
分别为直线AN,BN的斜率)恒成立?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=a-bcos![]() (b>0)的最大值为
(b>0)的最大值为![]() ,最小值为-
,最小值为-![]() .
.
(1)求a,b的值;
(2)求函数g(x)=-4asin![]() 的最小值并求出对应x的集合.
的最小值并求出对应x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
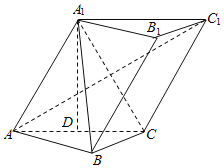
【题目】如图,三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=A1C=2,平面ACC1A1⊥平面ABC.现以边AC的中点D为坐标原点,平面ABC内垂直于AC的直线为![]() 轴,直线AC为
轴,直线AC为![]() 轴,直线DA1为
轴,直线DA1为![]() 轴建立空间直角坐标系,解决以下问题:
轴建立空间直角坐标系,解决以下问题:
(1)求异面直线AB与A1C所成角的余弦值;
(2)求直线AB与平面A1BC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,如图1.以
,如图1.以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.
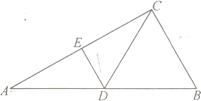
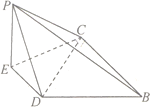
如图1 如图2
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下是某地搜集到的新房屋的销售价格![]() 和房屋的面积
和房屋的面积![]() 的数据:
的数据:
房屋面积( | 115 | 110 | 80 | 135 | 105 |
销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线;
(3)据(2)的结果估计当房屋面积为150![]() 时的销售价格.附:回归直线的斜率和截距的最小二乘法估计公式分别为:
时的销售价格.附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是海面上一条南北方向的海防警戒线,在
是海面上一条南北方向的海防警戒线,在 ![]() 上点
上点 ![]() 处有一个水声监测点,另两个监测点
处有一个水声监测点,另两个监测点 ![]() 分别在
分别在 ![]() 的正东方向
的正东方向 ![]() 处和
处和 ![]() 处.某时刻,监测点
处.某时刻,监测点 ![]() 收到发自目标
收到发自目标 ![]() 的一个声波,
的一个声波,![]() 后监测点
后监测点 ![]() 后监测点
后监测点 ![]() 相继收到这一信号,在当时的气象条件下,声波在水中的传播速度是
相继收到这一信号,在当时的气象条件下,声波在水中的传播速度是 ![]() .
.

(1)设 ![]() 到
到 ![]() 的距离为
的距离为 ![]() ,用
,用 ![]() 分别表示
分别表示 ![]() 到
到 ![]() 的距离,并求
的距离,并求 ![]() 的值;
的值;
(2)求目标 ![]() 的海防警戒线
的海防警戒线 ![]() 的距离(精确到
的距离(精确到 ![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com