
【题目】已知正数数列![]() 的前n项和为
的前n项和为![]() ,满足
,满足![]() ,
,![]() .
.
(1)求数列![]() 的通项公式,若
的通项公式,若![]() 恒成立,求k的范围;
恒成立,求k的范围;
(2)设![]() ,若
,若![]() 是递增数列,求实数a的取值范围.
是递增数列,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由![]() ,得
,得![]() =Sn﹣1+Sn﹣2,(n≥3).相减可得:
=Sn﹣1+Sn﹣2,(n≥3).相减可得:![]() =an+an﹣1,(n≥3),根据an>0,可得an﹣an﹣1=1(n≥3),当n=2时,
=an+an﹣1,(n≥3),根据an>0,可得an﹣an﹣1=1(n≥3),当n=2时,![]() =a1+a2+a1,解得
=a1+a2+a1,解得![]() ,进而得出an,利用裂项相消法化简
,进而得出an,利用裂项相消法化简![]() 恒成立,从而求出k的范围;
恒成立,从而求出k的范围;
(2)由(1)得![]() (n﹣1)2+a(n﹣1),利用
(n﹣1)2+a(n﹣1),利用![]() 是递增数列,可得bn+1﹣bn>0恒成立,即可实数a的取值范围.
是递增数列,可得bn+1﹣bn>0恒成立,即可实数a的取值范围.
(1)由![]() ,得
,得![]() =Sn-1+Sn﹣2,(n≥3).相减可得:
=Sn-1+Sn﹣2,(n≥3).相减可得:![]() =an+an﹣1(n≥3),
=an+an﹣1(n≥3),
∵an>0,∴an﹣1>0,∴平方差公式化简得an﹣an﹣1=1,(n≥3).
当n=2时,![]() =a1+a2+a1,且
=a1+a2+a1,且![]() ,∴
,∴![]() =2+
=2+![]() ,
,![]() >0,∴
>0,∴![]() =2或
=2或![]() =-1.因此当n=2时,an﹣an﹣1=1成立.
=-1.因此当n=2时,an﹣an﹣1=1成立.
∴数列{an}是以![]() 为首项,以1为公差的等差数列,∴an=1+n﹣1=n.
为首项,以1为公差的等差数列,∴an=1+n﹣1=n.
![]()
![]()
由题意得,k![]() .
.
(2)由(1)得,![]() =(n﹣1)2+a(n﹣1),
=(n﹣1)2+a(n﹣1),
∵![]() 是递增数列,∴bn+1﹣bn=n2+an﹣(n﹣1)2﹣a(n﹣1)=2n+a﹣1>0,
是递增数列,∴bn+1﹣bn=n2+an﹣(n﹣1)2﹣a(n﹣1)=2n+a﹣1>0,
即![]() 恒成立,∵
恒成立,∵![]() ,∴a
,∴a![]() ﹣1,∴实数a的取值范围是
﹣1,∴实数a的取值范围是![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() 为参数),A,B是C上的动点,且满足
为参数),A,B是C上的动点,且满足![]() (O为坐标原点),以原点O为极点,x轴的正半轴为极轴建立坐标系,点D的极坐标为
(O为坐标原点),以原点O为极点,x轴的正半轴为极轴建立坐标系,点D的极坐标为![]() .
.
(1)求椭圆C的极坐标方程和点D的直角坐标;
(2)利用椭圆C的极坐标方程证明 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位辆),若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆
轿车A | 轿车B | 轿车C | |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
(1)求下表中z的值;
(2)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:94,86,92,96,87,93,90,82把这8辆轿车的得分看作一个总体,从中任取一个得分数![]() 记这8辆轿车的得分的平均数为
记这8辆轿车的得分的平均数为![]() ,定义事件
,定义事件![]() {
{![]() ,且函数
,且函数![]() 没有零点},求事件
没有零点},求事件![]() 发生的概率
发生的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列说法:
①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;
②用相关指数R2来刻画回归的效果,R2值越大,说明模型的拟合效果越好;
③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型,拟合效果越好.
④在研究气温和热茶销售杯数的关系时,若求得相关指数R2≈0.85,则表明气温解释了15%的热茶销售杯数变化.
其中正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】统计学中,经常用环比、同比来进行数据比较,环比是指本期统计数据与上期比较,如![]() 年
年![]() 月与
月与![]() 年
年![]() 月相比,同比是指本期数据与历史同时期比较,如
月相比,同比是指本期数据与历史同时期比较,如![]() 年
年![]() 月与
月与![]() 年
年![]() 月相比.
月相比.
环比增长率![]() (本期数
(本期数![]() 上期数)
上期数)![]() 上期数
上期数![]() ,
,
同比增长率![]() (本期数
(本期数![]() 同期数)
同期数)![]() 同期数
同期数![]() .
.
下表是某地区近![]() 个月来的消费者信心指数的统计数据:
个月来的消费者信心指数的统计数据:
序号 |
|
|
|
|
|
|
|
|
时间 |
|
|
|
|
|
|
|
|
消费者信心指数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2017年
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]() 求该地区
求该地区![]() 年
年![]() 月消费者信心指数的同比增长率(百分比形式下保留整数);
月消费者信心指数的同比增长率(百分比形式下保留整数);
![]() 除
除![]() 年
年![]() 月以外,该地区消费者信心指数月环比增长率为负数的有几个月?
月以外,该地区消费者信心指数月环比增长率为负数的有几个月?
![]() 由以上数据可判断,序号
由以上数据可判断,序号![]() 与该地区消费者信心指数
与该地区消费者信心指数![]() 具有线性相关关系,写出
具有线性相关关系,写出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (
(![]() ,
,![]() 保留
保留![]() 位小数),并依此预测该地区
位小数),并依此预测该地区![]() 年
年![]() 月的消费者信心指数(结果保留
月的消费者信心指数(结果保留![]() 位小数,参考数据与公式:
位小数,参考数据与公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
, )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
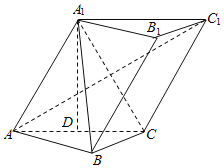
【题目】如图,三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=A1C=2,平面ACC1A1⊥平面ABC.现以边AC的中点D为坐标原点,平面ABC内垂直于AC的直线为![]() 轴,直线AC为
轴,直线AC为![]() 轴,直线DA1为
轴,直线DA1为![]() 轴建立空间直角坐标系,解决以下问题:
轴建立空间直角坐标系,解决以下问题:
(1)求异面直线AB与A1C所成角的余弦值;
(2)求直线AB与平面A1BC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图两个同心球,球心均为点![]() ,其中大球与小球的表面积之比为3:1,线段
,其中大球与小球的表面积之比为3:1,线段![]() 与
与![]() 是夹在两个球体之间的内弦,其中
是夹在两个球体之间的内弦,其中![]() 两点在小球上,
两点在小球上,![]() 两点在大球上,两内弦均不穿过小球内部.当四面体
两点在大球上,两内弦均不穿过小球内部.当四面体![]() 的体积达到最大值时,此时异面直线
的体积达到最大值时,此时异面直线![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则![]() ( )
( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com