
【题目】若函数g(x)=alnx,对任意x∈[1,e],都有g(x)≥﹣x2+(a+2)x恒成立,则实数a的取值范围是 .
【答案】a≤﹣1
【解析】解:由题意得到:a(x﹣lnx)≤x2﹣2x.
∵x∈[1,e],
∴lnx≤1≤x且等号不能同时取,所以lnx<x,即x﹣lnx<0,
因而a≤ ![]() (x∈[1,e])
(x∈[1,e])
令f(x)= ![]() ,(x∈[1,e]),
,(x∈[1,e]),
又g′(x)= ![]() ,
,
当x∈[1,e]时,x﹣1≥0,lnx≤1,x+2﹣2lnx>0,
从而g′(x)≥0(仅当x=1时取等号),
∴g(x)在[1,e]上为增函数,
∴g(x)的最小值为g(1)=﹣1,
∴a的取值范围是a≤﹣1.
所以答案是:a≤﹣1.
【考点精析】本题主要考查了函数的值域的相关知识点,需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能正确解答此题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】若直角坐标平面内两点P,Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称,则对称点(P,Q)是函数y=f(x)的一个“伙伴点组”(点对(P,Q)与(Q,P)看作同一个“伙伴点组”).则下列函数中,恰有两个“伙伴点组”的函数是(填空写所有正确选项的序号)
①y= ![]() ;②y=
;②y=  ;③y=
;③y= ![]() ;④y=
;④y=  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数fn(x)=﹣xn+3ax(a∈R,n∈N+),若对任意的x1 , x2∈[﹣1,1],都有|f3(x1)﹣f3(x2)|≤1,则a的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (a>0,且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是( )
(a>0,且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是( )
A.(0, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]∪{
]∪{ ![]() }
}
D.[ ![]() ,
, ![]() )∪{
)∪{ ![]() }
}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设![]() 是椭圆
是椭圆![]() 的左焦点,点
的左焦点,点![]() 是
是![]() 轴上的一点,点
轴上的一点,点![]() 为椭圆的左、右顶点,已知
为椭圆的左、右顶点,已知![]() ,且
,且![]()
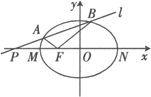
(1)求椭圆的标准方程;
(2)过点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,试判定直线
两点,试判定直线![]() 的斜率之和
的斜率之和![]() 是否为定值,并说明理由.
是否为定值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是_____________.
①.如果命题“![]() ”与命题“
”与命题“![]() 或
或![]() ”都是真命题,那么命题
”都是真命题,那么命题![]() 一定是真命题.
一定是真命题.
②.命题![]() ,则
,则![]()
③.命题“若![]() ,则
,则![]() ”的否命题是:“若
”的否命题是:“若![]() ,则
,则![]() ”
”
④.特称命题 “![]() ,使
,使![]() ”是真命题.
”是真命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=﹣2101 , 且当2≤n≤100时,an+2a102﹣n=3×2n恒成立,则数列{an}的前100项和S100= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知等差数列{an}的前n项和为Sn,且a3=5,S15="225."
(1)求数列{an}的通项an;
(2)设bn=![]() +2n,求数列{bn}的前n项和Tn.
+2n,求数列{bn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com