Question

如图，在斜三棱柱ABC-A₁B₁C₁中，四边形ABB₁A₁是菱形，四边形CBB₁C₁是矩形，AB⊥BC，CB=3，AB=4，∠A₁AB=60°，D、E分别是AC、A₁B的中点．
（Ⅰ）求证：平面CA₁B⊥平面ABB₁A₁；
（Ⅱ）求证：DE∥平面CBB₁C₁；
（Ⅲ）求四面体A₁ABC的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面平行的判定,平面与平面垂直的判定

专题：综合题,空间位置关系与距离

分析：（Ⅰ）由已知中四边形BCC₁B₁是矩形，AB⊥BC，我们易由线面垂直的判定定理得到CB⊥平面ABB₁A₁，再由面面垂直的判定定理，即可得到平面CA₁B⊥平面ABB₁A₁；
（Ⅱ）证明平面DEO∥平面CBB₁C₁，可得DE∥平面CBB₁C₁；
（Ⅲ）证明A₁O⊥平面ABC，可求四面体A₁ABC的体积．

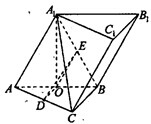
解答： （Ⅰ证明：∵四边形BCC₁B₁是矩形，AB⊥BC
∴AB⊥BC，BC⊥BB₁，AB∩BB₁=B
∴CB⊥平面ABB₁A₁，
∵CB?平面CA₁B
∴平面CA₁B⊥平面ABB₁A₁；
（Ⅱ）证明：取AB的中点O，连接OD，OE，则
∵D、E分别是AC、A₁B的中点，
∴OD∥BC，OE∥AA₁∥BB₁，
∵OD∩OE=O，BC∩BB₁=B，
∴平面DEO∥平面CBB₁C₁，
∵DE?平面DEO，
∴DE∥平面CBB₁C₁；
（Ⅲ）连接A₁O，则
∵四边形ABB₁A₁是菱形，∠A₁AB=60°，
∴A₁O⊥AB，
∵BC⊥平面ABB₁A₁，
∴BC⊥A₁O，
∵AB∩BC=B，
∴A₁O⊥平面ABC，
∴VA1ABC=

1

3

×(

1

2

×3×4)×2

3

=4

3

．

点评：本题考查的知识点是平面与平面垂直的判定，直线与平面平行的判定，其中等体积法，是转化思想在解答点到平面距离问题中最常用的方法．