
| A. | $\frac{1}{a}+\frac{1}{b}$=$\frac{1}{c}$ | B. | $\frac{2}{a}+\frac{1}{b}$=$\frac{2}{c}$ | C. | $\frac{1}{a}+\frac{2}{b}$=$\frac{1}{c}$ | D. | $\frac{1}{a}+\frac{1}{b}$=$\frac{2}{c}$ |
分析 设3a=4b=6c=k,k>0,则a=log3k,b=log4k,c=log6k,由此利用对数的性质、运算法则和换底公式能求出结果.
解答 解:∵实数a、b、c满足3a=4b=6c,
∴设3a=4b=6c=k,k>0,
则a=log3k,b=log4k,c=log6k,
在A中,$\frac{1}{a}+\frac{1}{b}$=logk3+logk4=logk12≠$lo{g}_{k}6=\frac{1}{c}$,故A错误;
在B中,$\frac{2}{a}+\frac{1}{b}$=2logk3+logk4=logk36=2logk6=$\frac{2}{c}$,故B正确;
在C中,$\frac{1}{a}+\frac{2}{b}$=logk3+2logk4=$lo{g}_{k}48=lo{g}_{k}6=\frac{1}{c}$,故C错误;
在D中,$\frac{1}{a}+\frac{1}{b}$=logk3+logk4=logk12≠2$lo{g}_{k}6=\frac{2}{c}$,故D错误.
故选:B.
点评 本题考查对数式化简求值,是基础题,解题时要认真审题,注意对数的性质、换底公式及运算法则的合理运用.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:解答题
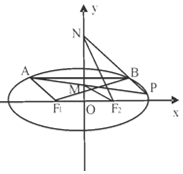 如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F1B|=4.
如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F1B|=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $-\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆 | B. | 直线 | C. | 射线 | D. | 线段 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com