
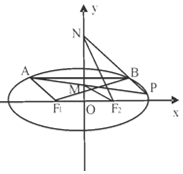
 如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F1B|=4.
如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F1B|=4.分析 (1)由题意焦距求得c,由对称性结合|F1A|+|F1B|=4可得2a,再由隐含条件求得b,则椭圆方程可求;
(2)设B(x0,y0),P(x1,y1),则A(-x0,y0),分别写出PA、PB所在直线方程,求出M、N的坐标,进一步求出MF2、NF2的斜率分别为k1、k2,结合A、B在椭圆上可得k1•k2是定值.
解答 解:(1)∵焦距$2\sqrt{2}$,∴2c=2$\sqrt{2}$,得c=$\sqrt{2}$,
由椭圆的对称性及已知得|F1A|=|F2B|,又∵|F1A|+|F1B|=4,|F1B|+|F2B|=4,
因此2a=4,a=2,于是b=$\sqrt{2}$,因此椭圆方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$;
(2)设B(x0,y0),P(x1,y1),则A(-x0,y0),
直线PA的方程为$y-{y}_{1}=\frac{{y}_{1}-{y}_{0}}{{x}_{1}+{x}_{0}}(x-{x}_{1})$,令x=0,得$y=\frac{{x}_{1}{y}_{0}+{x}_{0}{y}_{1}}{{x}_{1}+{x}_{0}}$,
故M(0,$\frac{{x}_{1}{y}_{0}+{x}_{0}{y}_{1}}{{x}_{1}+{x}_{0}}$);
直线PB的方程为$y-{y}_{1}=\frac{{y}_{1}-{y}_{0}}{{x}_{1}-{x}_{0}}(x-{x}_{1})$,令x=0,得$y=\frac{{x}_{1}{y}_{0}-{x}_{0}{y}_{1}}{{x}_{1}-{x}_{0}}$,
故N(0,$\frac{{x}_{1}{y}_{0}-{x}_{0}{y}_{1}}{{x}_{1}-{x}_{0}}$);
∴${k}_{1}=-\frac{{x}_{1}{y}_{0}+{x}_{0}{y}_{1}}{\sqrt{2}({x}_{1}+{x}_{0})}$,${k}_{2}=-\frac{{x}_{1}{y}_{0}-{x}_{0}{y}_{1}}{\sqrt{2}({x}_{1}-{x}_{0})}$,
因此${k}_{1}•{k}_{2}=\frac{1}{2}\frac{{{x}_{1}}^{2}{{y}_{0}}^{2}-{{x}_{0}}^{2}{{y}_{1}}^{2}}{{{x}_{1}}^{2}-{{x}_{0}}^{2}}$.
∵A,B在椭圆C上,∴${{y}_{1}}^{2}=2-\frac{{{x}_{1}}^{2}}{2},{{y}_{0}}^{2}=2-\frac{{{x}_{0}}^{2}}{2}$,
∴${k}_{1}{k}_{2}=\frac{1}{2}•\frac{{{x}_{1}}^{2}(2-\frac{1}{2}{{x}_{0}}^{2})-{{x}_{0}}^{2}(2-\frac{1}{2}{{x}_{1}}^{2})}{{{x}_{1}}^{2}-{{x}_{0}}^{2}}=1$.
点评 本题考查椭圆标准方程的求法,考查了直线与椭圆位置关系的应用,考查计算能力,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}+\frac{1}{b}$=$\frac{1}{c}$ | B. | $\frac{2}{a}+\frac{1}{b}$=$\frac{2}{c}$ | C. | $\frac{1}{a}+\frac{2}{b}$=$\frac{1}{c}$ | D. | $\frac{1}{a}+\frac{1}{b}$=$\frac{2}{c}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com