
���� ��1����{an}Ϊ�����ݼ����У��ɵ�������Ϊ99+98+��+1��
��2����nΪ����ʱ��a1��a3������a2n-1��0����nΪż��ʱ��0��a2��a4������a2n���ɵ���������
��3��������a1��a2����an�У���a1�����n-1��������p1������ԣ����У�n-1��-p1����������ԣ��ɵ�������an��an-1����a1�У�������Ϊ��n-1��-p1+��n-2��-p2+��+��n-n��-pn��
��� �⣺��1����{an}Ϊ�����ݼ����У���������Ϊ$99+98+��+1=\frac{��99+1����99}{2}=4950$��
��2����nΪ����ʱ��a1��a3������a2n-1��0��
��nΪż��ʱ��
$\begin{array}{l}{a_n}-{a_{n-2}}=-\frac{n}{n+1}+\frac{n-2}{n-1}��n��4��\\=\frac{-2}{{{n^2}-1}}\\=\frac{-2}{��n+1����n-1��}��0\end{array}$
��0��a2��a4������a2n��
��kΪ����ʱ��������Ϊ$��k-1��+��k-3��+��+2+\frac{k-3}{2}+\frac{k-5}{2}+��+1=\frac{{3{k^2}-4k+1}}{8}$��
��kΪż��ʱ��������Ϊ$��k-1��+��k-3��+��+1+\frac{k-2}{2}+\frac{k-4}{2}+��+1=\frac{{3{k^2}-2k}}{8}$��
��3��������a1��a2����an�У���a1�����n-1��������p1������ԣ�
���У�n-1��-p1����������ԣ�����������an��an-1����a1�У�
������Ϊ$��n-1��-{p_1}+��n-2��-{p_2}+��+��n-n��-{p_n}=\frac{n��n-1��}{2}-a$��
���� ���⿼���˵Ȳ����е�ͨ�ʽ�����ʽ���¶����������������˷������۷�����������������������������е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
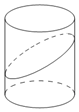 һ������뾶Ϊ2��Բ��������������ɽ���60���ƽ�����أ�������һ����Բ�������Բ�Ľ������$4\sqrt{3}$��
һ������뾶Ϊ2��Բ��������������ɽ���60���ƽ�����أ�������һ����Բ�������Բ�Ľ������$4\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $[\frac{1}{2}��1]$ | B�� | $��\frac{1}{2}��1]$ | C�� | $��\frac{1}{2}��{log_3}2]$ | D�� | $[\frac{1}{2}��{log_3}2]$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
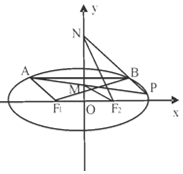 ��ͼ��F1��F2�ֱ�����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬�ҽ���Ϊ2$\sqrt{2}$������ABƽ����x�ᣬ��|F1A|+|F1B|=4��
��ͼ��F1��F2�ֱ�����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬�ҽ���Ϊ2$\sqrt{2}$������ABƽ����x�ᣬ��|F1A|+|F1B|=4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com