
分析 (1)化简函数f(x)为分段函数,然后求出an=f(n)=n+3.
(2)如果{an}是等差数列,求出公差d,首项,然后求解a的范围.
(3)当a≥-1时,求出前n项和,当-2≤a≤-1时,当a≤-2时,分别求出n项和即可.
解答 (18分)解:(1)∵函数f(x)=2|x+2|-|x+1|=$\left\{\begin{array}{l}{x+3,x≥-1}\\{3x+5,-2<x≤-1}\\{-x-3,x≤-2}\end{array}\right.$,…(2分)
又n≥1且n∈N*,∴an=f(n)=n+3.…(4分)
(2)如果{an}是等差数列,则an-an-1=d,an=an-1+d,
由f(x)知一定有an=an-1+3,公差d=3.
当a1≥-1时,符合题意.
当-2≤a1≤-1时,a2=3a1+5,由a2-a1=3得3a1+5-a1=3,得a1=-1,a2=2.
当a1≤-2时,a2=-a1-3,由a2-a1=3得-a1-3-a1=3,得a1=-3,此时a2=0.
综上所述,可得a的取值范围是a≥-1或a=-3.…(9分)
(3)当a≥-1时,an=f(an-1)=an-1+3,∴数列{an}是以a为首项,公差为3的等差数列,${S_n}=na+\frac{n(n-1)}{2}×3=\frac{3}{2}{n^2}+(a-\frac{3}{2})n$.…(12分)
当-2≤a≤-1时,a2=3a1+5=3a+5≥-1,∴n≥3时,an=an-1+3.∴n=1时,S1=a.n≥2时,${S_n}=a+(n-1){a_2}+\frac{(n-1)(n-2)}{2}×3=\frac{3}{2}{n^2}+(\frac{1}{2}+3a)n-2a-2$
又S1=a也满足上式,∴${S_n}=\frac{3}{2}{n^2}+(\frac{1}{2}+3a)n-2a-2$(n∈N*)…(15分)
当a≤-2时,a2=-a1-3=-a-3≥-1,∴n≥3时,an=an-1+3.∴n=1时,S1=a.n≥2时,${S_n}=a+(n-1){a_2}+\frac{(n-1)(n-2)}{2}×3=\frac{3}{2}{n^2}-(a+\frac{15}{2})n+2a+6$
又S1=a也满足上式,∴${S_n}=\frac{3}{2}{n^2}-(a+\frac{15}{2})n+2a+6$(n∈N*).
综上所述:Sn=$\left\{\begin{array}{l}{\frac{3}{2}{n}^{2}+(a-\frac{3}{2})n,a≥-1}\\{\frac{3}{2}{n}^{2}+(\frac{1}{2}+3a)n-2a-2,-2<a≤-1}\\{\frac{3}{2}{n}^{2}-(a+\frac{15}{2})n+2a+6,a≤-2}\end{array}\right.$.…(18分).
点评 本题考查数列的递推关系式的应用,数列求和,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | $[{0,\frac{π}{3}}]∪[{\frac{π}{2},\frac{3π}{4}}]$ | B. | $[{0,\frac{π}{3}}]∪(\frac{3π}{4},π)$ | C. | $[{\frac{π}{3},\frac{π}{2}}]∪(\frac{3π}{4},π]$ | D. | $[{0,\frac{π}{3}}]∪(\frac{π}{2},\frac{3π}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{1}{2},1]$ | B. | $(\frac{1}{2},1]$ | C. | $(\frac{1}{2},{log_3}2]$ | D. | $[\frac{1}{2},{log_3}2]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
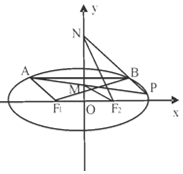 如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F1B|=4.
如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F1B|=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $-\frac{7}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com