
分析 根据对称函数的定义,结合h(x)≥g(x)恒成立,转化为点到直线的距离d≥1,利用点到直线的距离公式进行求解即可.
解答 解:解:∵x∈D,点(x,g(x)) 与点(x,h(x))都关于点(x,f(x))对称,∴g(x)+h(x)=2f(x),∵h(x)≥g(x)恒成立,
∴2f(x)=g(x)+h(x)≥g(x)+g(x)=2g(x),即f(x)≥g(x)恒成立,
作出g(x)和f(x)的图象,
若h(x)≥g(x)恒成立,
则h(x)在直线f(x)的上方,
即g(x)在直线f(x)的下方,
则直线f(x)的截距b>0,且原点到直线y=2x+b的距离d≥1,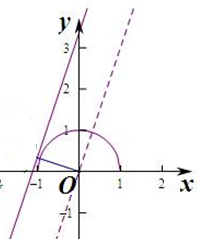
d=$\frac{|b|}{\sqrt{{2}^{2}+1}}=\frac{|b|}{\sqrt{5}}≥1$⇒b≥$\sqrt{5}$或b$≤-\sqrt{5}$(舍去)
即实数b的取值范围是[$\sqrt{5}$,+∞),
点评 本题主要考查不等式恒成立问题,根据对称函数的定义转化为点到直线的距离关系,利用数形结合是解决本题的关键.综合性较强,有一定的难度.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{1}{2},1]$ | B. | $(\frac{1}{2},1]$ | C. | $(\frac{1}{2},{log_3}2]$ | D. | $[\frac{1}{2},{log_3}2]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
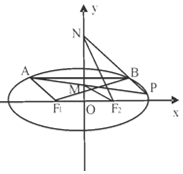 如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F1B|=4.
如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F1B|=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 99 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com