练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．作出函数y=$\left\{\begin{array}{l}{{x}^{2}-6x+7，（2＜x≤5）}\\{-2x-2，（-4＜x≤2）}\end{array}\right.$的图象，并求出其定义域和值域，写出其单调增区间和单调减区间．

    分析 分段作出函数y=$\left\{\begin{array}{l}{{x}^{2}-6x+7，（2＜x≤5）}\\{-2x-2，（-4＜x≤2）}\end{array}\right.$的图象，从而写出其定义域和值域及单调增区间和单调减区间．

    解答 解：作函数y=$\left\{\begin{array}{l}{{x}^{2}-6x+7，（2＜x≤5）}\\{-2x-2，（-4＜x≤2）}\end{array}\right.$的图象如下，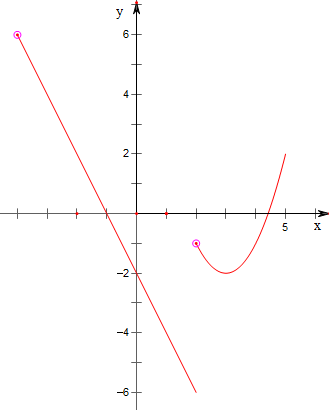

    结合图象可知，
    其定义域为（-4，5]，值域为[-6，6）；
    其单调增区间为[3，5]，单调减区间为（-4，2]，（2，3）．

    点评 本题考查了分段函数的综合应用及函数的图象的作法与应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    15．如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD=2PD，PD⊥底面ABCD．
    （1）证明：PA⊥BD；
    （2）若PD=AD，求PA与面PBD所成的角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．等比数列{an}中，a1=2，a3=8，则S4=-10或30．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．对于定义在D上的函数y=f（x），若同时满足
    ①存在闭区间[a，b]⊆D，使得任取x1∈[a，b]，都有f（x1）=c（c是常数）；
    ②对于D内任意x2，当x2∉[a，b]时总有f（x2）＞c，则称f（x）为“平底型”函数．
    判断f1（x）=|2x-1|+|2x-2|，f2（x）=|2x-1|-|2x-2|是否是“平底型”函数？简要说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知二次函数f（x）在y轴上的截距为3，且满足f（x+2）-f（x）=4x+2．
    （1）求f（x）的单调递增区间；
    （2）在区间[-2，2]上，y=f（x）图象恒在直线y=-3x+m上方，试确定实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x}，x＞1}\\{{3}^{x}，x≤1}\end{array}\right.$，则f（2）+f（-2）=$\frac{37}{9}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知f（x）=x2+$\frac{a}{{x}^{2}}$，是否存在实数a，使f（x）在（0，2]上单调递减，在（2，+∞） 上单调递增？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．求函数f（x）=$\sqrt{2{x}^{2}+x-3}+lo{g}_{3}（3+2x-{x}^{2}）$的定义域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．求下列函数的定义域：
    （1）y=$\frac{1}{lg（x+1）-3}$；
    （2）y=$\sqrt{lo{g}_{a}（4x-3）}$（a＞0，且a≠1）．

    查看答案和解析>>

    同步练习册答案