练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．某超市随机选取1000位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如下统计表，其中“√”表示购买，“×”表示未购买．
    甲乙丙丁
    100√×√√
    217×√×√
    200√√√×
    300√×√×
    85√×××
     98×√××
    （1）估计顾客同时购买乙和丙的概率；
    （2）估计顾客在甲、乙、丙、丁中同时购买3种商品的概率；
    （3）如果顾客购买了甲，则该顾客同时购买乙、丙、丁中哪种商品的可能性最大？

    分析 （1）从统计表可得，在这1000名顾客中，同时购买乙和丙的有200人，从而求得顾客同时购买乙和丙的概率．
    （2）根据在甲、乙、丙、丁中同时购买3种商品的有300人，求得顾客顾客在甲、乙、丙、丁中同时购买3种商品的概率．
    （3）在这1000名顾客中，求出同时购买甲和乙的概率、同时购买甲和丙的概率、同时购买甲和丁的概率，从而得出结论．

    解答 解：（1）从统计表可得，在这1000名顾客中，同时购买乙和丙的有200人，
    故顾客同时购买乙和丙的概率为$\frac{200}{1000}$=0.2．
    （2）在这1000名顾客中，在甲、乙、丙、丁中同时购买3种商品的有100+200=300（人），
    故顾客顾客在甲、乙、丙、丁中同时购买3种商品的概率为$\frac{300}{1000}$=0.3．
    （3）在这1000名顾客中，同时购买甲和乙的概率为$\frac{200}{1000}$=0.2，
    同时购买甲和丙的概率为$\frac{100+200+300}{1000}$=0.6，
    同时购买甲和丁的概率为$\frac{100}{1000}$=0.1，
    故同时购买甲和丙的概率最大．

    点评 本题主要考查古典概率、互斥事件的概率加法公式的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1 （a＞0，b＞0）的一条渐近线过点（2，$\sqrt{3}$），且双曲线的一个焦点在抛物线y2=4$\sqrt{7}$x的准线上，则双曲线的方程为（　　）
    A．$\frac{{x}^{2}}{21}$-$\frac{{y}^{2}}{28}$=1B．$\frac{{x}^{2}}{28}$-$\frac{{y}^{2}}{21}$=1C．$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1D．$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．在平面直角坐标系xOy中，圆O：x2+y2=1，P为直线l：x=t（1＜t＜2）上一点．
    （1）已知t=$\frac{4}{3}$．
    ①若点P在第一象限，且OP=$\frac{5}{3}$，求过点P的圆O的切线方程；
    ②若存在过点P的直线交圆O于点A，B，且B恰为线段AP的中点，求点P纵坐标的取值范围；
    （2）设直线l与x轴交于点M，线段OM的中点为Q，R为圆O上一点，且RM=1，直线RM与圆O交于另一点N，求线段NQ长的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．如图，在△ABC中，AB=AC，△ABC的外接圆⊙O的弦AE交BC于点D．
    求证：△ABD∽△AEB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=ln$\frac{1+x}{1-x}$，
    （Ⅰ）求曲线y=f（x）在点（0，f（0））处的切线方程；
    （Ⅱ）求证，当x∈（0，1）时，f（x）＞$2（x+\frac{{x}^{3}}{3}）$；
    （Ⅲ）设实数k使得f（x）$＞k（x+\frac{{x}^{3}}{3}）$对x∈（0，1）恒成立，求k的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．在直角坐标系xOy中，曲线C1：$\left\{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}\right.$（t为参数，t≠0），其中0≤α≤π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=2sinθ，C3：ρ=2$\sqrt{3}$cosθ．
    （1）求C2与C3交点的直角坐标；
    （2）若C1与C2相交于点A，C1与C3相交于点B，求|AB|的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费xi和年销售量yi（i=1，2，…，8）数据作了初步处理，得到下面的散点图及一些统计量的值．

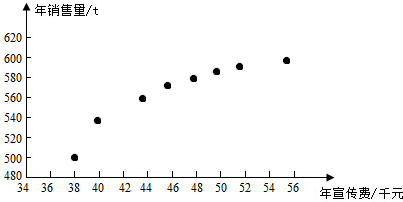
    $\overline{x}$$\overline{y}$$\overline{w}$$\sum _{i=1}^{8}$（xi-$\overline{x}$）2$\sum _{i=1}^{8}$（wi-$\overline{w}$）2$\sum _{i=1}^{8}$（xi-$\overline{x}$）（yi-$\overline{y}$）$\sum _{i=1}^{8}$（wi-$\overline{w}$）（yi-$\overline{y}$）
    46.65636.8289.81.61469108.8
    表中wi=$\sqrt{x}$i，$\overline{w}$=$\frac{1}{8}$$\sum _{i=1}^{8}w{\;}_{i}$
    （Ⅰ）根据散点图判断，y=a+bx与y=c+d$\sqrt{x}$哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）
    （Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；
    （Ⅲ）已知这种产品的年利润z与x、y的关系为z=0.2y-x．根据（Ⅱ）的结果回答下列问题：
    （i）年宣传费x=49时，年销售量及年利润的预报值是多少？
    （ii）年宣传费x为何值时，年利润的预报值最大？
    附：对于一组数据（u1 v1），（u2 v2）…..（un vn），其回归线v=α+βu的斜率和截距的最小二乘估计分别为：$\widehat{β}$=$\frac{\sum_{i=1}^{n}（{u}_{1}-\overline{u}）（{v}_{1}-\overline{v}）}{\sum_{i=1}^{n}（{u}_{1}-\overline{u}）^{2}}$，$\widehat{α}$=$\overline{v}$-$\widehat{β}$$\overline{u}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．如图，已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形，AA1=6，且AA1⊥底面ABCD，点P、Q分别在棱DD1、BC上．
    （1）若P是DD1的中点，证明：AB1⊥PQ；
    （2）若PQ∥平面ABB1A1，二面角P-QD-A的余弦值为$\frac{3}{7}$，求四面体ADPQ的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．设a，b＞0，a+b=5，则$\sqrt{a+1}$+$\sqrt{b+3}$的最大值为3$\sqrt{2}$．

    查看答案和解析>>

    同步练习册答案