
分析 根据条件可判断函数为奇函数,不等式可整理为m<(x2-1)(6-x)恒成立,利用构造函数h(x)=(x2-1)(6-x),通过求导函数判断函数的单调性,得出函数的最小值.
解答 解:$f(x)=lg(x+\sqrt{{x^2}+1})$的定义域为R,且f(-x)=-f(x),
所以f(x)为奇函数,显然在(0,+∞)上为单调递增函数,
∴函数在R上也为递增函数,
∵f($\frac{x+1}{x-1}$)+f($\frac{m}{{{{(x-1)}^2}(6-x)}}$)>0,即f($\frac{x+1}{x-1}$)>-f($\frac{m}{{{{(x-1)}^2}(6-x)}}$),
∴f($\frac{x+1}{x-1}$)>f(-$\frac{m}{{{{(x-1)}^2}(6-x)}}$),
∴$\frac{x+1}{x-1}$>-$\frac{m}{(x-1)^{2}(6-x)}$,
∴m>(x2-1)(x-6)恒成立,
设h(x)=(x2-1)(x-6),h'(x)=3x2-12x-1=3(x-2)2-13,
∴h'(x)<0,函数递减,函数的最大值为h(1)=0,
∴m>0.
故答案为m>0.
点评 考查了奇函数的判断和恒成立问题的转化.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{10}}}{3}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
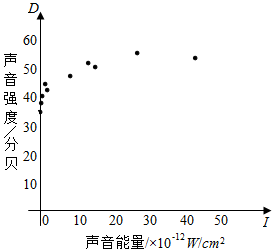 噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了解强度D(单位:分贝)与声音能量I(单位:W/cm2)之间的关系,将测量得到的声音强度Di和声音能量Ii(i=1,2…,10)数据作了初步处理,得到如表的散点图及一些统计量的值.
噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了解强度D(单位:分贝)与声音能量I(单位:W/cm2)之间的关系,将测量得到的声音强度Di和声音能量Ii(i=1,2…,10)数据作了初步处理,得到如表的散点图及一些统计量的值.| $\overline{I}$ | $\overline{D}$ | $\overline{W}$ | $\underset{\stackrel{10}{∑}}{i=1}({I}_{i}-\overline{I})^{2}$ | $\underset{\stackrel{10}{∑}}{i=1}({W}_{i}-\overline{W})^{2}$ | $\underset{\stackrel{10}{∑}}{i=1}({I}_{i}-\overline{I})({D}_{i}-\overline{D})$ | $\underset{\stackrel{10}{∑}}{i=1}({W}_{i}-\overline{W})({D}_{i}-\overline{D})$ |
| 1.04×10-11 | 45.7 | -11.5 | 1.56×10-21 | 0.51 | 6.88×10-11 | 5.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com