
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{10}}}{3}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{10}$ |
分析 求出直线的方程和双曲线的渐近线方程,通过解方程组得出xC,xB,根据等比中项的性质列方程化简得出a,b的关系.代入离心率公式计算.
解答 解:抛物线的焦点为F(a,0),
∴直线方程为y=-x+a.
∵双曲线$\frac{x^2}{a^2}-\frac{x^2}{b^2}$=1的渐近线为y=±$\frac{b}{a}x$,
∴直线y=-x+a与渐近线的交点横坐标分别为$\frac{{a}^{2}}{a-b}$,$\frac{{a}^{2}}{a+b}$.
∵xC是xB与xF的等比中项,
∴($\frac{{a}^{2}}{a+b}$)2=a•$\frac{{a}^{2}}{a-b}$或($\frac{{a}^{2}}{a-b}$)2=a$•\frac{{a}^{2}}{a+b}$,
∴3ab+b2=0(舍)或3ab-b2=0,∴b=3a.
∴c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{10}a$,
∴双曲线的离心率e=$\frac{c}{a}$=$\sqrt{10}$.
故选:D.
点评 本题考查了抛物线与双曲线的性质,直线的交点坐标,等比中项,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,一楼高AB为17.5m,某广告公司在楼顶安装一块高BC为2m的广告牌,安装过程中,工作人员利用一个高EF为1.5m的仪器检测安装效果,设AE=xm,该仪器观察到广告牌的视角∠BFC=θ.
如图,一楼高AB为17.5m,某广告公司在楼顶安装一块高BC为2m的广告牌,安装过程中,工作人员利用一个高EF为1.5m的仪器检测安装效果,设AE=xm,该仪器观察到广告牌的视角∠BFC=θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
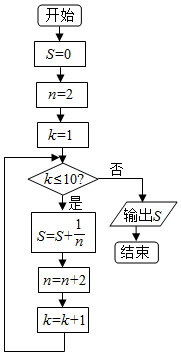
| A. | S=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{10}$ | B. | S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$ | ||
| C. | S=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{11}$ | D. | S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{22}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
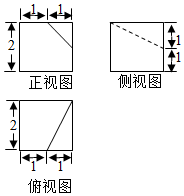
| A. | $\frac{23}{3}$cm3 | B. | $\frac{22}{3}$cm3 | C. | $\frac{47}{6}$cm3 | D. | 7cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com