
分析 (1)在Rt△ABC中,C=90°,A=60°,可得三边之比为:1:$\sqrt{3}$:2,即可判断出真假.
(2)由S=$\frac{1}{2}$absin$\frac{π}{3}$=$\frac{\sqrt{3}}{4}$ab,若面积是整数,则存在正整数x,使得$\sqrt{3}$ab=4x,此式不成立,即可判断出真假.
(3)设C=$\frac{π}{3}$,可得a+b+c=12,c2=a2+b2-2ab$cos\frac{π}{3}$,化为$(\sqrt{ab})^{2}$-16$\sqrt{ab}$+48≥0,解出即可判断出真假.
(4)设C=$\frac{π}{3}$=C1,对边分类讨论:①若夹角$\frac{π}{3}$的两条边分别相等,可得此两个三角形全等;②若夹角$\frac{π}{3}$其中一条边相等,由于面积相等,夹角$\frac{π}{3}$另一条边必然相等,此两个三角形全等.
解答 解:(1)若Rt△ABC中,C=90°,A=60°,则三边之比为:1:$\sqrt{3}$:2,因此不存在直角三角形是“完美三角形,因此(1)是假命题;
(2)由S=$\frac{1}{2}$absin$\frac{π}{3}$=$\frac{\sqrt{3}}{4}$ab,若面积是整数,则存在正整数x,使得$\sqrt{3}$ab=4x,由于a,b都为整数,此式不成立,因此不存在面积都是整数的“完美三角形”,(2)是真命题;
(3)设C=$\frac{π}{3}$,则a+b+c=12,c2=a2+b2-2ab$cos\frac{π}{3}$,可得(12-a-b)2=a2+b2-ab,
化为$(\sqrt{ab})^{2}$-16$\sqrt{ab}$+48≥0,解得0<$\sqrt{ab}$≤4,即ab≤16,当且仅当a=b=4时取等号,
可得周长为12的“完美三角”中面积最大为$\frac{1}{2}×16×\frac{\sqrt{3}}{2}$=4$\sqrt{3}$,是真命题;
(4)设C=$\frac{π}{3}$=C1,①若夹角$\frac{π}{3}$的两条边分别相等,满足条件,则此两个三角形全等;
②若夹角$\frac{π}{3}$其中一条边相等,由于面积相等,夹角$\frac{π}{3}$另一条边必然相等,可得:此两个三角形全等.因此是真命题.
以上真命题有(2)(3)(4).
故答案为:(2)(3)(4).
点评 本题考查了解三角形、余弦定理、三角形面积计算公式、基本不等式的性质、新定义、简易逻辑的判定方法、不等式的解法,考查了推理能力与计算能力,属于中档题.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:选择题
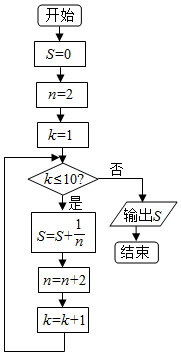
| A. | S=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{10}$ | B. | S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$ | ||
| C. | S=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{11}$ | D. | S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{22}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
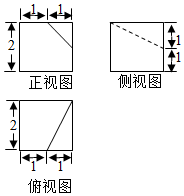
| A. | $\frac{23}{3}$cm3 | B. | $\frac{22}{3}$cm3 | C. | $\frac{47}{6}$cm3 | D. | 7cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2<b2 | B. | ab<b2 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | (${\frac{1}{2}}$)a<(${\frac{1}{2}}$)b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 参与调查问卷次数 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10) | [10,12] |
| 参与调查问卷人数 | 8 | 14 | 8 | 14 | 10 | 6 |
| P(x2>k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3,841 | 6.635 |
| 男 | 女 | 合计 | |
| 积极上网参政居民 | 8 | ||
| 不积极上网参政居民 | |||
| 合计 | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com