
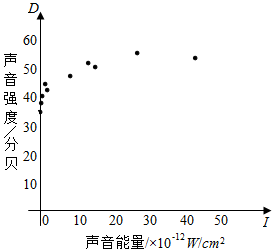
 噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了解强度D(单位:分贝)与声音能量I(单位:W/cm2)之间的关系,将测量得到的声音强度Di和声音能量Ii(i=1,2…,10)数据作了初步处理,得到如表的散点图及一些统计量的值.
噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了解强度D(单位:分贝)与声音能量I(单位:W/cm2)之间的关系,将测量得到的声音强度Di和声音能量Ii(i=1,2…,10)数据作了初步处理,得到如表的散点图及一些统计量的值.| $\overline{I}$ | $\overline{D}$ | $\overline{W}$ | $\underset{\stackrel{10}{∑}}{i=1}({I}_{i}-\overline{I})^{2}$ | $\underset{\stackrel{10}{∑}}{i=1}({W}_{i}-\overline{W})^{2}$ | $\underset{\stackrel{10}{∑}}{i=1}({I}_{i}-\overline{I})({D}_{i}-\overline{D})$ | $\underset{\stackrel{10}{∑}}{i=1}({W}_{i}-\overline{W})({D}_{i}-\overline{D})$ |
| 1.04×10-11 | 45.7 | -11.5 | 1.56×10-21 | 0.51 | 6.88×10-11 | 5.1 |
分析 (I)利用回归系数公式先求出D关于w的回归方程,再转化为D关于I的回归方程;
(Ⅱ)利用对数的运算性质和基本不等式求出I的最小值,计算$\stackrel{∧}{D}$的最小值.
解答 解:(I)$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{10}({w}_{i}-\overline{w})({D}_{i}-\overline{D})}{\sum_{i=1}^{10}({w}_{i}-\overline{w})^{2}}$=$\frac{5.1}{0.51}=10$,$\stackrel{∧}{a}$=$\overline{D}$-$\stackrel{∧}{b}$$\overline{w}$=45.7-10×(-11.5)=160.7.
∴D关于w的线性回归方程为$\stackrel{∧}{D}$=10w+160.7,
∴D关于I的回归方程为$\stackrel{∧}{D}$=10lgI+160.7.
(II)∵$\frac{1}{{I}_{1}}$+$\frac{4}{{I}_{2}}$=1010,
∴I=I1+I2=10-10($\frac{1}{{I}_{1}}+\frac{4}{{I}_{2}}$)(I1+I2)=10-10(5+$\frac{{I}_{2}}{{I}_{1}}$+$\frac{4{I}_{1}}{{I}_{2}}$)≥9×10-10.
∴$\stackrel{∧}{D}$=10lg(9×10-10)+160.7=10lg9+60.7≥60.
∴点P会受到噪声污染的干扰.
点评 本题考查了回归方程的求解,对数的运算性质及回归方程应用.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{7}$ | B. | $\frac{5}{3}$ | C. | $\frac{11}{7}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<c<a | B. | c<b<a | C. | a<c<b | D. | a<b<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com