思路解析：结合平面几何知识，圆心必在两圆交点的垂直平分线上，易求圆心坐标，可解;也可以考虑利用圆系方程.
解法一：由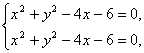
得
∴
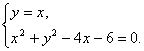
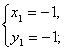
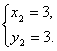
∴两圆x2+y2-4x-6=0和x2+y2-4y-6=0的交点分别为A（-1，-1）、B（3，3）.
∴线段AB的垂直平分线方程为y-1=-(x-1).
由
得
∴所求圆的圆心为（3,-1）,半径为
=4.
∴所求圆的方程为（x-3）2+(y+1)2=16.
解法二：同解法一求得A(-1,-1)、B(3,3).设所求圆的方程为(x-a)2+(y-b)2=r2，则
∴
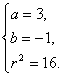
∴所求圆的方程为（x-3）2+(y+1)2=16.
解法三：设经过已知两圆的交点的圆的方程为x2+y2-4x-6+λ(x2+y2-4y-6)=0(λ≠-1),则其圆心坐标为（
,
）.
∵所求圆的圆心在直线x-y-4=0上，
∴
-
-4=0,λ=-
.
∴所求圆的方程为x2+y2-4x-6-
(x2+y2-4y-6)=0,
即x2+y2-6x+2y-6=0.
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com