
| A. | $\frac{1}{{e}^{2}}$<x1x2<$\frac{1}{e}$ | B. | $\frac{1}{{e}^{2}}$<x1x2<1 | C. | $\frac{1}{e}$<x1x2<1 | D. | e<x1x2<e2 |
分析 求出f(x)的导数,求得在x=0处的切线的斜率,由两直线垂直的条件:斜率之积为-1,可得k的值,令g(x)=0,则|lnx|=2e-x,作出y=|lnx|和y=2e-x的图象,可知恰有两个交点,设零点为x1,x2且|lnx1|>|lnx2|,再结合零点存在定理,可得结论.
解答  解:f(x)=ke-x在的导数为f′(x)=-ke-x,
解:f(x)=ke-x在的导数为f′(x)=-ke-x,
在点x=0处的切线斜率为k=-k,
由切线与直线x-2y-1=0垂直,可得-k=-2,
解得k=2,则f(x)=2e-x,
令g(x)=0,则|lnx|=2e-x,
作出y=|lnx|和y=2e-x的图象,
可知恰有两个交点,
设零点为x1,x2且|lnx1|>|lnx2|,0<x1<1,x2>1,
故有$\frac{1}{{x}_{1}}$>x2,即x1x2<1.
又g($\frac{1}{{e}^{2}}$)=2${e}^{-\frac{1}{{e}^{2}}}$-2<0,g($\frac{1}{e}$)=2${e}^{-\frac{1}{e}}$-1>0,
可得$\frac{1}{{e}^{2}}$<x1<$\frac{1}{e}$,
即x1x2>$\frac{1}{{e}^{2}}$,
即有$\frac{1}{{e}^{2}}$<x1x2<1.
故选:B.
点评 本题考查函数的零点与方程根的关系,考查数形结合的数学思想,考查学生分析解决问题的能力,正确作出函数图象是关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{6}})$ | B. | $({0,\frac{1}{6}})∪({\frac{5}{6},\frac{5}{2}})$ | C. | $({0,\frac{1}{4}})∪({\frac{5}{4},\frac{5}{2}})$ | D. | $({0,\frac{1}{4}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值为1,图象关于直线x=$\frac{π}{2}$对称 | B. | 在(0,$\frac{π}{4}$)上单调递减,为奇函数 | ||
| C. | 在(-$\frac{3π}{8}$,$\frac{π}{8}$)上单调递增,为偶函数 | D. | 周期为π,图象关于点($\frac{3π}{8}$,0)对称 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:解答题
设有关于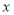 的一元二次方程
的一元二次方程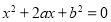 .
.
(Ⅰ)若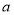 是从
是从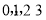 四个数中任取的一个数,
四个数中任取的一个数,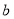 是从
是从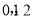 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(Ⅱ)若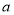 是从区间
是从区间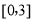 任取的一个数,
任取的一个数,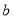 是从区间
是从区间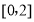 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com