
某超市在节日期间进行有奖促销,凡在该超市购物满300元的顾客,将获得一次摸奖机会,规则如下:
奖盒中放有除颜色外完全相同的1个红球,1个黄球,1个白球和1个黑球.顾客不放回的每次摸出1个球,若摸到黑球则停止摸奖,否则就要将奖盒中的球全部摸出才停止.规定摸到红球奖励10元,摸到白球或黄球奖励5元,摸到黑球不奖励.
(Ⅰ)求1名顾客摸球3次停止摸奖的概率;
(Ⅱ)记 为1名顾客摸奖获得的奖金数额,求随机变量
为1名顾客摸奖获得的奖金数额,求随机变量 的分布列和数学期望.
的分布列和数学期望.
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:高中数学 来源: 题型:解答题
2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》。其中规定:居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米。某城市环保部门随机抽取了一居民区去年20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
| 组别 | PM2.5浓度 (微克/立方米 | 频数(天) | 频率 |
| 第一组 | (0,25] | 5 | 0.25 |
| 第二组 | (25,50] | 10 | 0.5 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100) | 2 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在盒子里有大小相同,仅颜色不同的乒乓球共10个,其中红球5个,白球3个,蓝球2个。现从盒子中每次任意取出一个球,若取出的是蓝球则结束,若取出的不是蓝球则将其放回箱中,并继续从箱中任意取出一个球,但取球次数最多不超过3次。求:
(1)取两次就结束的概率;
(2)正好取到2个白球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
高三年级有3名男生和1名女生为了报某所大学,事先进行了多方详细咨询,并根据自己的高考成绩情况,最终估计这3名男生报此所大学的概率都是 ,这1名女生报此所大学的概率是
,这1名女生报此所大学的概率是 .且这4人报此所大学互不影响。
.且这4人报此所大学互不影响。
(Ⅰ)求上述4名学生中报这所大学的人数中男生和女生人数相等的概率;
(Ⅱ)在报考某所大学的上述4名学生中,记 为报这所大学的男生和女生人数的和,试求
为报这所大学的男生和女生人数的和,试求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市为了推动全民健身运动在全市的广泛开展,该市电视台开办了健身竞技类栏目《健身大闯关》,规定参赛者单人闯关,参赛者之间相互没有影响,通过关卡者即可获奖。现有甲、乙、丙 人参加当天的闯关比赛,已知甲获奖的概率为
人参加当天的闯关比赛,已知甲获奖的概率为 ,乙获奖的概率为
,乙获奖的概率为 ,丙获奖而甲没有获奖的概率为
,丙获奖而甲没有获奖的概率为 。
。
(Ⅰ)求三人中恰有一人获奖的概率;
(Ⅱ)求三人中至少有两人获奖的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
袋子A、B中均装有若干个大小相同的红球和白球,从A中摸出一个红球的概率是 ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(1) 从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止。
①求恰好摸5次停止的概率;
②记5次之内(含5次)摸到红球的次数为 ,求随机变量
,求随机变量 的分布列及数学期望。
的分布列及数学期望。
(2)若A、B两个袋子中的球数之比为1:2,将A、B中的球装在一起后,从中摸出一个红球的概率是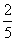 ,求p的值。
,求p的值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一个盒子中,放有标号分别为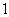 ,
,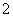 ,
,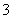 的三个小球,现从这个盒子中,有放回地先后抽得两个小球的标号分别为
的三个小球,现从这个盒子中,有放回地先后抽得两个小球的标号分别为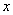 、
、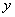 ,设
,设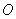 为坐标原点,设
为坐标原点,设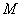 的坐标为
的坐标为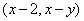 .
.
(1)求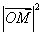 的所有取值之和;
的所有取值之和;
(2)求事件“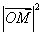 取得最大值”的概率.
取得最大值”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校为调查高二年级学生的身高情况,按随机抽样的方法抽取200名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有48人.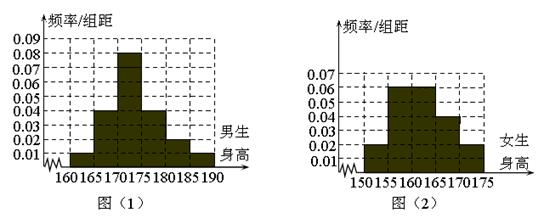 (Ⅰ)在抽取的学生中,身高不超过165cm的男、女生各有多少人?并估计男生的平均身高。
(Ⅰ)在抽取的学生中,身高不超过165cm的男、女生各有多少人?并估计男生的平均身高。
(Ⅱ)在上述200名学生中,从身高在170~175cm之间的学生按男、女性别分层抽样的方法,抽出7人,从这7人中选派4人当旗手,求4人中至少有一名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2012年3月2日,江苏卫视推出全新益智答题类节目《一站到底》,甲、乙两人报名参加《一站到底》面试的初试选拔,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题.规定每次抢答都从备选题中随机抽出3题进行测试,至少答对2题初试才能通过.
(Ⅰ)求甲答对试题数ξ的概率分布及数学期望;
(Ⅱ)求甲、乙两人至少有一人初试通过的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com