
【题目】(重点班)我们知道对数函数![]() ,对任意
,对任意![]() ,都有
,都有![]() 成立,若
成立,若![]() ,则当
,则当![]() 时,
时,![]() .参照对数函数的性质,研究下题:定义在
.参照对数函数的性质,研究下题:定义在![]() 上的函数
上的函数![]() 对任意
对任意![]() ,都有
,都有![]() ,并且当且仅当
,并且当且仅当![]() 时,
时,![]() 成立.
成立.
(1)设![]() ,求证:
,求证:![]() ;
;
(2)设![]() ,若
,若![]() ,比较
,比较![]() 与
与![]() 的大小.
的大小.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,把两个全等的![]() 和
和![]() 分别置于平面直角坐标系中,使直角边
分别置于平面直角坐标系中,使直角边![]() 在
在![]() 轴上,已知点
轴上,已知点![]() ,过
,过![]() 两点的直线分别交
两点的直线分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() . 抛物线
. 抛物线![]() 经过
经过![]() 三点.
三点.
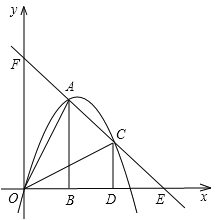
(1)求该抛物线的函数解析式;
(2)点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的平行线交抛物线于点
轴的平行线交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,问是否存在这样的点
,问是否存在这样的点![]() ,使得四边形
,使得四边形![]() 为等腰梯形?若存在,求出此时点
为等腰梯形?若存在,求出此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)若![]() 沿
沿![]() 方向平移(点
方向平移(点![]() 始终在线段
始终在线段![]() 上,且不与点
上,且不与点![]() 重合),
重合),![]() 在平移的过程中与
在平移的过程中与![]() 重叠部分的面积记为
重叠部分的面积记为![]() ,试探究
,试探究![]() 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其指标值来衡量,其指标值越大表明质量越好,且指标值大于或等于102的产品为优质品.现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做试验,各生产了100件这种产品,并测量了每件产品的指标值,得到了下面的试验结果:
配方)做试验,各生产了100件这种产品,并测量了每件产品的指标值,得到了下面的试验结果:
![]() 配方的频数分布表
配方的频数分布表
指标值分组 |
|
|
|
|
|
频数 | 8 | 20 | 42 | 22 | 8 |
![]() 配方的频数分布表
配方的频数分布表
指标值分组 |
|
|
|
|
|
频数 | 4 | 12 | 42 | 32 | 10 |
(Ⅰ)分别估计用![]() 配方,
配方,![]() 配方生产的产品的优质品率;
配方生产的产品的优质品率;
(Ⅱ)已知用![]() 配方生产的一件产品的利润
配方生产的一件产品的利润![]() (单位:元)与其指标值
(单位:元)与其指标值![]() 的关系式为
的关系式为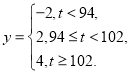
估计用![]() 配方生产的一件产品的利润大于0的概率,并求用
配方生产的一件产品的利润大于0的概率,并求用![]() 配方生产的上述产品平均每件的利润。
配方生产的上述产品平均每件的利润。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 截以原点
截以原点![]() 为圆心的圆所得的弦长为
为圆心的圆所得的弦长为![]() 。
。
(1)求圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 切于第一象限,且与坐标轴交于点
切于第一象限,且与坐标轴交于点![]() ,当
,当![]() 长最小时,求直线
长最小时,求直线![]() 的方程;
的方程;
(3)设![]() 是圆
是圆![]() 上任意两点,点
上任意两点,点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,若直线
,若直线![]() 分别交
分别交![]() 轴于点
轴于点![]() 和
和![]() ,问
,问![]() 是否为定值?若是,请求出该定值;若不是,请说明理由。
是否为定值?若是,请求出该定值;若不是,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】尧盛机械生产厂每生产某产品![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为
(万元),其中固定成本为![]() 万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本).销售收入
万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本).销售收入![]() (万元)满足
(万元)满足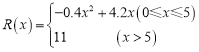 ,假定生产的产品都能卖掉,请完成下列问题:
,假定生产的产品都能卖掉,请完成下列问题:
(1)写出利润函数![]() 的解析式(注:利润=销售收入-总成本);
的解析式(注:利润=销售收入-总成本);
(2)试问该工厂生产多少台产品时,可使盈利最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查200名50岁以上有吸烟习惯与患慢性气管炎的人的情况,获数据如下
患慢性气管炎 | 未患慢性气管炎 | 总计 | |
吸烟 |
| 30 | 100 |
不吸烟 | 35 |
| 100 |
合计 | 105 | 95 | 200 |
(1)表中![]() ,
,![]() 的值分别是多少;
的值分别是多少;
(2)试问:有吸烟习惯与患慢性气管炎病是否有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某镇计划建造一个室内面积为800m2的矩形蔬菜温室,在温室内,沿左、右两侧与后侧内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地.当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com