
【题目】已知z0=2+2i,|z-z0|=![]() .
.
(1)求复数z在复平面内的对应点的轨迹;
(2)求z为何值时|z|有最小值,并求出|z|的最小值.
【答案】(1)复数z点的轨迹为以z0(2,2)为圆心,![]() 为半径的圆.(2)当z=1+i时,|z|min=
为半径的圆.(2)当z=1+i时,|z|min=![]()
【解析】分析:(1)设![]() ,由
,由![]() ,化简即可得到复数在复平面内对应的点的轨迹;
,化简即可得到复数在复平面内对应的点的轨迹;
(2)由(1)可知当复数![]() 点在
点在![]() 的连线上时,
的连线上时,![]() 有最大值或最小值,即可得到结果.
有最大值或最小值,即可得到结果.
详解:(1)设z=x+yi(x,y∈R),由|z-z0|=![]() ,
,
得:|x+yi-(2+2i)|=|(x-2)+(y-2)i|=![]() ,.
,.
解得:(x-2)2+(y-2)2=2...
∴复数z点的轨迹为以z0(2,2)为圆心,![]() 为半径的圆...
为半径的圆...
(2)当z点在Oz0的连线上时,|z|有最大值或最小值..
∵|Oz0|=2![]() ,半径为
,半径为![]() .
.
∴当z=1+i时,|z|min=![]() ..
..


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A. 一条直线与一个平面平行,它就和这个平面内的任意一条直线平行
B. 平行于同一个平面的两条直线平行
C. 平面外的两条平行直线中的一条与一个平面平行,则另一条直线也与此平面平行
D. 与两个相交平面的交线平行的直线,必平行于这两个平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了![]() 名观众进行调查,如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于
名观众进行调查,如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于![]() 分钟的观众称为体育迷.
分钟的观众称为体育迷.
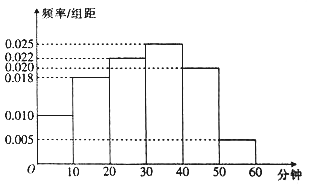
(1)以频率为概率,若从这![]() 名观众中随机抽取
名观众中随机抽取![]() 名进行调查,求这
名进行调查,求这![]() 名观众中体育迷人数
名观众中体育迷人数![]() 的分布列;
的分布列;
(2)若抽取![]() 人中有女性
人中有女性![]() 人,其中女体育迷有
人,其中女体育迷有![]() 人,完成答题卡中的列联表并判断能否在犯错概率不超过
人,完成答题卡中的列联表并判断能否在犯错概率不超过![]() 的前提下认为是体育迷与性别有关系吗?
的前提下认为是体育迷与性别有关系吗?
附表及公式:
|
|
|
|
|
|
|
|
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某宾馆安排![]() 五人入住3个房间,每个房间至少住1人,且
五人入住3个房间,每个房间至少住1人,且![]() 不能住同一房间,则不同的安排方法有( )种
不能住同一房间,则不同的安排方法有( )种
A. 64 B. 84 C. 114 D. 144
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…[80,90],并整理得到如下频率分布直方图: 
(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B两样本的下列数字特征对应相同的是
A. 众数 B. 平均数 C. 中位数 D. 标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据.
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)试根据(1)求出的线性回归方程,预测燃放烟花爆竹的天数为9的雾霾天数.
相关公式: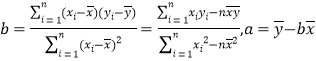
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=x2的图象在点(x0 , x02)处的切线为l,若l也与函数y=lnx,x∈(0,1)的图象相切,则x0必满足( )
A.0<x0< ![]()
B.![]() <x0<1
<x0<1
C.![]() <x0<
<x0< ![]()
D.![]() <x0
<x0 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点. (Ⅰ)证明:A1O⊥平面ABC;
(Ⅱ)求二面角A﹣A1B﹣C1的大小.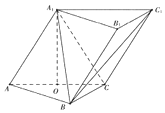
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com