[题目]下列命题正确的是( )A. 一条直线与一个平面平行.它就和这个平面内的任意一条直线平行B. 平行于同一个平面的两条直线平行C. 平面外的两条平行直线中的一条与一个平面平行.则另一条直线也与此平面平行D. 与两个相交平面的交线平行的直线.必平行于这两个平面题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】下列命题正确的是( )

A. 一条直线与一个平面平行，它就和这个平面内的任意一条直线平行

B. 平行于同一个平面的两条直线平行

C. 平面外的两条平行直线中的一条与一个平面平行，则另一条直线也与此平面平行

D. 与两个相交平面的交线平行的直线，必平行于这两个平面

【答案】C

【解析】

逐一考查所给的说法是否正确即可.

在正方体中逐一考查所给的命题：

A. 直线AB平行于平面，不满足，题中的命题错误；

B. 直线AB,BC为平行于同一个平面的两条直线，很明显两直线相交不平行，题中的命题错误；

C. 由线面平行的判定定理可知：平面外的两条平行直线中的一条与一个平面平行，则另一条直线也与此平面平行，题中的命题正确；

D. 与两个相交平面的交线平行的直线，不一定平行于这两个平面，可能在某个平面之内，题中的命题错误；

本题选择C选项.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某班从6名干部中（其中男生4人，女生2人）选3人参加学校的义务劳动．
（1）设所选3人中女生人数为ξ，求ξ的分布列及Eξ；
（2）求男生甲或女生乙被选中的概率；
（3）在男生甲被选中的情况下，求女生乙也被选中的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数（）在处取得极值．

（1）求的单调区间；

（2）讨论的零点个数，并说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知圆心在x轴正半轴上的圆C与直线相切，与y轴交于M，N两点，且．

Ⅰ求圆C的标准方程；

Ⅱ过点的直线l与圆C交于不同的两点D，E，若时，求直线l的方程；

Ⅲ已知Q是圆C上任意一点，问：在x轴上是否存在两定点A，B，使得？若存在，求出A，B两点的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在一个港口，相邻两次高潮发生时间相距，低潮时水的深度为，高潮时为，一次高潮发生在10月10日4:00，每天涨潮落潮时，水的深度与时间近似满足关系式.

（1）若从10月10日0:00开始计算时间，选用一个三角函数来近似描述该港口的水深和时间之间的函数关系.

（2）10月10日17:00该港口水深约为多少？（精确到）

（3）10月10日这一天该港口共有多长时间水深低于？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知f（x）=（x2﹣2ax）lnx+2ax﹣ x2 ，其中a∈R．
（1）若a=0，且曲线f（x）在x=t处的切线l过原点，求直线l的方程；
（2）求f（x）的极值；
（3）若函数f（x）有两个极值点x1 ， x2（x1＜x2），证明f（x1）+f（x2）＜ a2+3a．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某种产品的质量以其质量指标值衡量，并依据质量指标值划分等极如下表：

质量指标值m	m＜185	185≤m＜205	m≥205
等级	三等品	二等品	一等品

从某企业生产的这种产品中抽取200件，检测后得到如下的频率分布直方图：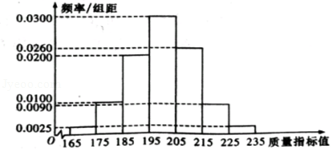

（Ⅰ）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定？
（Ⅱ）在样本中，按产品等极用分层抽样的方法抽取8件，再从这8件产品中随机抽取4件，求抽取的4件产品中，一、二、三等品都有的概率；
（III）该企业为提高产品质量，开展了“质量提升月”活动，活动后再抽样检测，产品质量指标值X近似满足X～N（218，140}），则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少？