
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
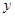 (万元)与处理量
(万元)与处理量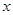 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: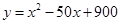 ,且每处理一吨废弃物可得价值为
,且每处理一吨废弃物可得价值为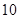 万元的某种产品,同时获得国家补贴
万元的某种产品,同时获得国家补贴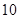 万元.
万元.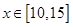 时,判断该项举措能否获利?如果能获利,求出最大利润;
时,判断该项举措能否获利?如果能获利,求出最大利润;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 立方米,且
立方米,且 . 假设该容器的建造费用仅与其表面积有关. 已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为22千元. 设该容器的建造费用为y千元. 当该容器建造费用最小时,r的值为( )
. 假设该容器的建造费用仅与其表面积有关. 已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为22千元. 设该容器的建造费用为y千元. 当该容器建造费用最小时,r的值为( )
A. | B.1 | C. | D.2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
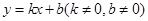 ;②
;② ;③
;③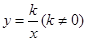 ;④
;④ .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 =x2+
=x2+ ,求f(x);
,求f(x);查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,则n的取值集合是________.
,则n的取值集合是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com