
分析 对于①,直接据反例进行判断;
对于②和③,利用数列中an与Sn的关系式求出数列的通项,由等差数列和等比数列的定义加以验证;
对于④依题意,可得公差d>0,从而可判断④正确.
解答 解:①如:数列0、0、0、…,是等差数列但不是等比数列,则①不正确;
②由Sn=an2+bn,(a,b∈R),当n=1时,a1=S1=a+b,
当n≥2时,an=Sn-Sn-1=an2+bn-[a(n-1)2+b(n-1)]=2an-a+b.
当n=1时a1适合上式.
∴an=2an-a+b.满足an+1-an=2a为常数,则{an}是等差数列,
当{an}是等差数列时,Sn=na1+$\frac{n(n-1)}{2}$d=$\frac{d}{2}$n2+(a1-$\frac{d}{2}$)n,
即为Sn=an2+bn(a,b∈R)形式,成立,则②正确;
③若Sn=1-(-1)n,当n=1时,a1=S1=2,
当n≥2时,an=Sn-Sn-1=1-(-1)n-[1-(-1)n-1]=(-1)n+1+(-1)n-1,
当n为奇数时,an=2.当n为偶数时,an=-2.
所以{an}是等比数列,则③正确;
④一个等差数列{an}中,若存在ak+1>ak>0(k∈N*),由ak+1=ak+d知ak+d>ak>0,
故d>0,所以,对于任意自然数n>k,都有an>0,则④正确;
故答案为:②③④.
点评 本题考查命题的真假判断与应用,差数列和等比数列的定义,以及数列中an与Sn的关系式应用,解答的关键在于对基础知识的理解与掌握.


科目:高中数学 来源: 题型:选择题
| A. | p∨q为假命题 | B. | p∧q为真命题 | C. | ¬p∧q为真命题 | D. | ¬p∨¬q是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,5} | B. | {3,6} | C. | {2,5,6} | D. | {2,3,5,6,8} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x≤6} | B. | {1,2,3,4,5,6} | C. | {2,3,4,5,6} | D. | {2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ABC=90°,AB=$\sqrt{3}$,BC=1,AA1=3,BD⊥AC,M为线段CC1上一点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ABC=90°,AB=$\sqrt{3}$,BC=1,AA1=3,BD⊥AC,M为线段CC1上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
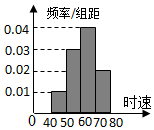 关于统计数据的分析,有以下几个结论:
关于统计数据的分析,有以下几个结论:| A. | 2 | B. | 1 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{10}+\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{10}-\sqrt{2}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x≤3} | B. | {x|x<-2或x>4} | C. | {x|-3≤x≤4} | D. | {x|x<-3或x>4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com