
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ABC=90°,AB=$\sqrt{3}$,BC=1,AA1=3,BD⊥AC,M为线段CC1上一点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ABC=90°,AB=$\sqrt{3}$,BC=1,AA1=3,BD⊥AC,M为线段CC1上一点.分析 (Ⅰ)推导出BD⊥AM,AM⊥平面A1BD.从而能求出当CM=时1,AM⊥平面A1BD.
(Ⅱ)方法一:在(Ⅰ)的条件下,BD⊥平面ACC1A1,BD⊥AM,设A1D∩AM=N,则∠BND即为二面角B-AM-C的平面角,由此能求出二面角B-AM-C的正切值.
(Ⅱ)方法二:以B为原点,BC,BA,BB1为x,y,z轴建立空间直角坐标系,利用向量法能求出二面角B-AM-C的正切值.
解答 (本小题满分12分)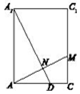
证明:(Ⅰ)在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,
∴平面ACC1A1⊥平面ABC.
∵BD⊥AC,∴BD⊥平面ACC1A1,∴BD⊥AM.
∵∠ABC=90°,$AB=\sqrt{3}\;\;,\;\;BC=1$,
∴$BD=\frac{{\sqrt{3}}}{2}\;\;,\;\;AD=\frac{3}{2}\;\;,\;\;CD=\frac{1}{2}$.…(2分)
在平面ACC1A1内,当△A1AD∽△ACM即可满足AM⊥A1D,此时,AM⊥平面A1BD.…(4分)
∴$\frac{CM}{AC}=\frac{AD}{{A{A_1}}}$,∴$\frac{CM}{2}=\frac{{\frac{3}{2}}}{3}$,∴CM=1,AM⊥平面A1BD.…(6分)
解:(Ⅱ)方法一: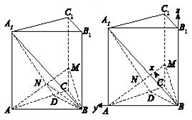 在(Ⅰ)的条件下,BD⊥平面ACC1A1,BD⊥AM,
在(Ⅰ)的条件下,BD⊥平面ACC1A1,BD⊥AM,
设A1D∩AM=N,则∠BND即为二面角B-AM-C的平面角.…(8分)Rt△ACM中,
∴$\frac{CM}{DN}=\frac{AM}{AD}$,∴$DN=\frac{{3\sqrt{5}}}{10}$.…(10分)
Rt△BDN中,$BD=\frac{{\sqrt{3}}}{2}$,$DN=\frac{{3\sqrt{5}}}{10}$,$tan∠BND=\frac{BD}{DN}=\frac{{\sqrt{15}}}{3}$,
二面角B-AM-C的正切值为$\frac{{\sqrt{15}}}{3}$.…(12分)
(Ⅱ)方法二:以B为原点,BC,BA,BB1为x,y,z轴建立如图空间直角坐标系.
B(0,0,0),A(0,$\sqrt{3}$,0),C(1,0,0),M(1,0,1),D($\frac{3}{4},\frac{\sqrt{3}}{4},0$).
$\overrightarrow{MA}=({-1\;\;,\;\;\sqrt{3}\;\;,\;\;-1})$,$\overrightarrow{MB}=({-1\;\;,\;\;0\;\;,\;\;-1})$.…(8分)
在(Ⅰ)的条件下,BD⊥平面ACC1A1,∴BD⊥平面ACM,$\overrightarrow{BD}=({\frac{3}{4}\;\;,\;\;\frac{{\sqrt{3}}}{4}\;\;,\;\;0})$.
设n⊥平面ABM,n=(x,y,z),$\left\{\begin{array}{l}n⊥\overrightarrow{MA}\\ N⊥\overrightarrow{MB}\end{array}\right.$
即$\left\{\begin{array}{l}1-x+\sqrt{3}y-z=0\\ 1-x-z=0\end{array}\right.$,则n=(1,0,-1),…(10分)
设二面角B-AM-C的平面角为θ,$cosθ=\frac{{n•\overrightarrow{BD}}}{{|n|•|{\overrightarrow{BD}}|}}=\frac{{\sqrt{6}}}{4}$,
所以二面角B-AM-C的正切值为$\frac{{\sqrt{15}}}{3}$.…(12分)
点评 本题考查线面垂直的证明,考查二面角的正切值的求不地,是中档题,解题时要认真审题,注意空间维能力的培养.


科目:高中数学 来源: 题型:选择题
| A. | {1,3,6,7,8} | B. | {1,3,7,8} | C. | {3,7,8} | D. | {0,1,2,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
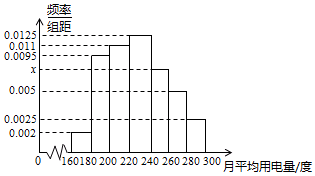 某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com