
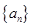 的前
的前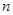 项和为
项和为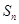 ,且
,且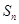 满足
满足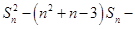
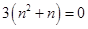 ,
,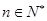 .
.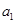 的值;
的值;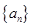 的通项公式;
的通项公式;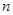 ,有
,有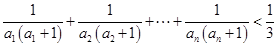 .
.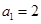 ;(2)
;(2)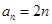 ;(3)详见解析.
;(3)详见解析.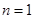 代入方程
代入方程 得到
得到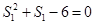 ,结合题中条件(数列
,结合题中条件(数列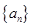 的各项均为正数,得到
的各项均为正数,得到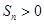 )求出
)求出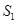 的值,从而得到
的值,从而得到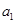 的值;(2)由十字相乘法结合
的值;(2)由十字相乘法结合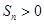 得到
得到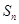 的表达式,然后在
的表达式,然后在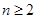 的情况下,由
的情况下,由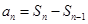 求出数列
求出数列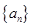 的表达式,并验证
的表达式,并验证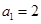 是否满足该表达式,从而得到数列
是否满足该表达式,从而得到数列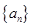 的通项公式;(3)解法一是利用放缩法得到
的通项公式;(3)解法一是利用放缩法得到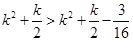
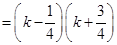 ,于是得到
,于是得到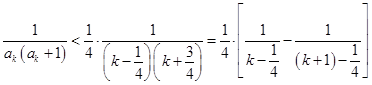 ,最后利用裂项求和法证明题中的不等式;解法二是保持
,最后利用裂项求和法证明题中的不等式;解法二是保持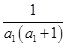 不放缩,在
不放缩,在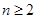 的条件下放缩为
的条件下放缩为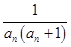
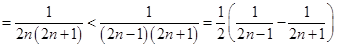 ,最后在
,最后在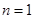 和
和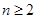 时利用放缩法结合裂项法证明相应的不等式.
时利用放缩法结合裂项法证明相应的不等式.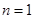 得:
得: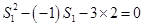 ,即
,即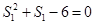 ,
,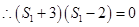 ,
,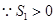 ,
, ,即
,即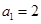 ;
; ,得
,得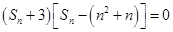 ,
,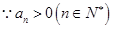 ,
,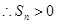 ,从而
,从而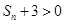 ,
,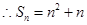 ,
,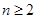 时,
时, ,
,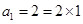 ,
,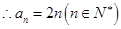 ;
;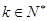 时,
时,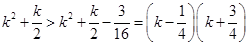 ,
,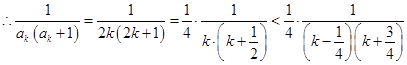
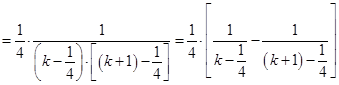
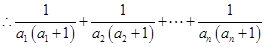

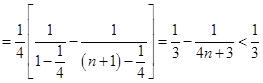 .
.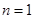 时,
时,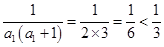 成立,
成立,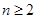 时,
时,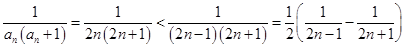 ,
,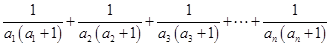
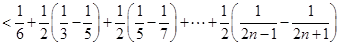
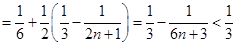 .
.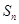 与
与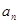 的关系考查数列通项的求解,以及利用放缩法证明数列不等式的综合问题,考查学生的计算能力与逻辑推理能力,属于中等偏难题.
的关系考查数列通项的求解,以及利用放缩法证明数列不等式的综合问题,考查学生的计算能力与逻辑推理能力,属于中等偏难题.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:单选题
 ,且an=f(n)+f(n+1),则a1+a2+a3+…+a2014等于( )
,且an=f(n)+f(n+1),则a1+a2+a3+…+a2014等于( )| A.-2013 | B.-2014 | C.2013 | D.2014 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com