
 ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点。
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点。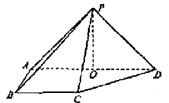
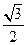 ?若存在,求出
?若存在,求出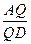 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。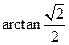
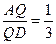 ,理由见解析。
,理由见解析。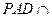 平面ABCD=AD,
平面ABCD=AD,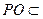 平面PAD,
平面PAD,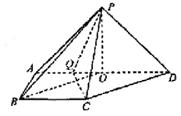
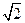 ,
,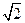 ,AO=1,所以OP=1,
,AO=1,所以OP=1,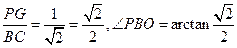 。
。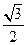 。
。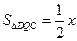 ,由(Ⅱ)得CD=OB=
,由(Ⅱ)得CD=OB=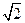 ,
,
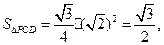
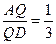 。
。 的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系O-xyz,依题意,易得A(0,-1,0),B(1,-1,0),C(1,0,0),D(0,1,0),
的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系O-xyz,依题意,易得A(0,-1,0),B(1,-1,0),C(1,0,0),D(0,1,0),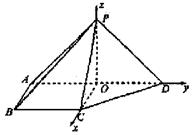
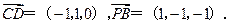
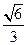 ,
,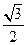 ,
,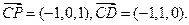
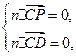 所以
所以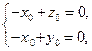 即
即 ,
,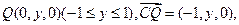 由
由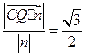 ,得
,得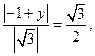 解y=-
解y=-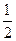 或y=
或y=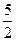 (舍去),
(舍去),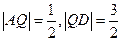 ,所以存在点Q满足题意,此时
,所以存在点Q满足题意,此时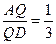 .
.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
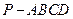 中,侧面PDC是边长为2的正三角形,且与底面
中,侧面PDC是边长为2的正三角形,且与底面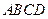 垂直,底面ABCD是面积为
垂直,底面ABCD是面积为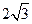 的菱形,
的菱形,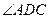 为锐角,M为PB的中点。
为锐角,M为PB的中点。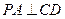
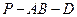 的大小
的大小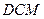 的距离
的距离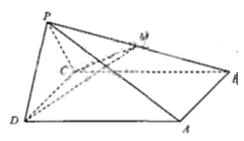
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
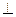 平面ABEF,如图所示,FD
平面ABEF,如图所示,FD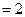 , AD=1, EF=
, AD=1, EF=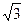 .
.
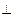 平面FCB;
平面FCB;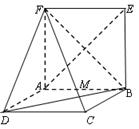
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 为菱形,
为菱形,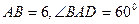 ,两个正三棱锥
,两个正三棱锥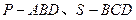 (底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,点
(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,点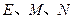 分别在
分别在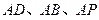 上,且
上,且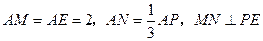 .
.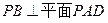 ;
;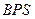 与底面
与底面 所成锐二面角的平面角的正切值;
所成锐二面角的平面角的正切值; 的体积.
的体积. 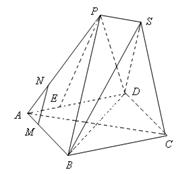
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点
升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点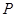 (图2)。有下列四个命题:
(图2)。有下列四个命题:| A.正四棱锥的高等于正四棱柱高的一半 |
B.将容器侧面水平放置时,水面也恰好过点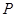 |
C.任意摆放该容器,当水面静止时,水面都恰好经过点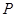 |
D.若往容器内再注入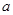 升水,则容器恰好能装满 升水,则容器恰好能装满 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
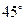 纬线上有A,B两点,设该纬线圈上A,B两点的劣弧长为
纬线上有A,B两点,设该纬线圈上A,B两点的劣弧长为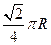 ,(R为地球半径),则A,B两点间的球面距离为__________________.
,(R为地球半径),则A,B两点间的球面距离为__________________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com