
分析 (Ⅰ)利用二倍角与两角和的余弦函数化简函数为一个角的一个三角函数的形式,通过正弦函数的单调减区间,直接求函数f(x)的单调递增区间;
(Ⅱ)设BC=a,则AC=$\sqrt{3}$a,利用余弦定理求出cosB,求出cos2B和sin2B,再利用三角形的面积公式化简S2△ABC,利用配方法和二次函数的性质求出面积的最大值.
解答 解:(Ⅰ)f(x)=2sin2(x-$\frac{π}{4}$)+$\sqrt{3}$cos2x-3
=2×$\frac{1-cos(2x-\frac{π}{2})}{2}$+$\sqrt{3}$cos2x-3=-sin2x+$\sqrt{3}$cos2x-2
=-2sin(2x-$\frac{π}{3}$)-2
由$\frac{π}{2}$+2kπ≤2x-$\frac{π}{3}$≤$\frac{3π}{2}$+2kπ,
得$\frac{5π}{12}$+kπ≤x≤$\frac{11}{12}$π+kπ(k∈Z).
∴函数f(x)的单调递增区间是[$\frac{5π}{12}$+kπ,$\frac{11}{12}$π+kπ](k∈Z).
(Ⅱ)AB=2|f($\frac{π}{4}$)|=2|-1-2|=6,设BC=a,则AC=$\sqrt{3}$a,
根据余弦定理得,cosB=$\frac{36+{a}^{2}-3{a}^{2}}{2×6×a}$=$\frac{3}{a}$-$\frac{1}{6}$a,
则sin2B=1-cos2B=2-$\frac{9}{{a}^{2}}$-$\frac{1}{36}{a}^{2}$,
根据面积公式得,S△ABC=$\frac{1}{2}•6•a•$sinB=3asinB,
所以S2△ABC=9a2sin2B=-$\frac{1}{4}$(a2-36)2+243,
当a2=36,即a=6时,S2△ABC取到最大值243,即△ABC面积的最大值是9$\sqrt{3}$.
点评 本题考查二倍角公式与两角和与差的三角函数,函数的单调性函数值的求法,考查计算能力,转化思想.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
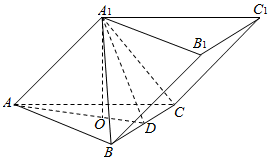 已知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,顶点A1在底面ABC上的射影O是△ABC的中心,AA1与AB的夹角为45°
已知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,顶点A1在底面ABC上的射影O是△ABC的中心,AA1与AB的夹角为45°查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{25}{36}$ | D. | $\frac{11}{36}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$+1 | B. | $\frac{{1+\sqrt{3}}}{2}$ | C. | 2 | D. | $\frac{{1+\sqrt{5}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com