
【题目】如图,在平面直角坐标系xOy中,已知椭圆 ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,焦点到相应准线的距离为1.
,焦点到相应准线的距离为1. 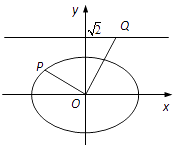
(1)求椭圆的标准方程;
(2)若P为椭圆上的一点,过点O作OP的垂线交直线 ![]() 于点Q,求
于点Q,求 ![]() 的值.
的值.
【答案】
(1)解:由题意得, ![]() ,
, ![]() ,
,
解得 ![]() ,c=1,b=1.
,c=1,b=1.
所以椭圆的方程为 ![]()
(2)解:由题意知OP的斜率存在.
当OP的斜率为0时, ![]() ,
, ![]() ,所以
,所以 ![]() .
.
当OP的斜率不为0时,设直线OP方程为y=kx.
由 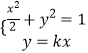 得(2k2+1)x2=2,解得
得(2k2+1)x2=2,解得 ![]() ,所以
,所以 ![]() ,
,
所以 ![]() .
.
因为OP⊥OQ,所以直线OQ的方程为 ![]() .
.
由 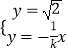 得
得 ![]() ,所以OQ2=2k2+2.
,所以OQ2=2k2+2.
所以 ![]() .
.
综上,可知 ![]()
【解析】(1)由已知条件可得 ![]() ,
, ![]() ,然后求解椭圆的方程.(2)由题意知OP的斜率存在.当OP的斜率为0时,求解结果;当OP的斜率不为0时,设直线OP方程为y=kx.联立方程组,推出
,然后求解椭圆的方程.(2)由题意知OP的斜率存在.当OP的斜率为0时,求解结果;当OP的斜率不为0时,设直线OP方程为y=kx.联立方程组,推出 ![]() .OQ2=2k2+2.然后求解即可.
.OQ2=2k2+2.然后求解即可.
【考点精析】通过灵活运用椭圆的标准方程,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 即可以解答此题.
即可以解答此题.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (0<φ<π)
(0<φ<π)
(1)当φ![]() 时,在给定的坐标系内,用“五点法”做出函数f(x)在一个周期内的图象;
时,在给定的坐标系内,用“五点法”做出函数f(x)在一个周期内的图象;
(2)若函数f(x)为偶函数,求φ的值;
(3)在(2)的条件下,求函数在[﹣π,π]上的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(1)求一续保人本年度的保费高于基本保费的概率;
(2)已知一续保人本年度的保费高于基本保费,求其保费比基本保费高出![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校200名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这200名学生的平均分;
(3)若这200名学生的数学成绩中,某些分数段的人数![]() 与英语成绩相应分数段的人数
与英语成绩相应分数段的人数![]() 之比如下表所示,求英语成绩在
之比如下表所示,求英语成绩在![]() 的人数.
的人数.
分数段 |
|
|
|
|
|
| 1:2 | 2:1 | 6:5 | 1:2 | 1:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了参加某运动会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源人数如下表:
队别 | 北京 | 上海 | 天津 | 八一 |
人数 | 4 | 6 | 3 | 5 |
(1)从这18名队员中随机选出两名,求两人来自同一队的概率;
(2)若要求选出两名队员担任正副队长,设其中来自北京队的人数为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应党的十九大所提出的教育教学改革,某校启动了数学教学方法的探索,学校将髙一年级部分生源情况基本相同的学生分成甲、乙两个班,每班40人,甲班按原有传统模式教学,乙班实施自主学习模式.经过一年的教学实验,将甲、乙两个班学生一年来的数学成绩取平均数,两个班学生的平均成绩均在[50,100],按照区间[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀,



![]() ,
,
(I)完成表格,并判断是否有90%以上的把握认为“数学成绩优秀与教学改革有关”

〔Ⅱ)从乙班[70,80),[80,90),[90,100]分数段中,按分层抽样随机抽取7名学生座谈,
从中选三位同学发言,记来自[80,90)发言的人数为随机变量x,求x的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,P为棱C1D1的中点,Q为棱BB1上的点,且BQ=λBB1(λ≠0). 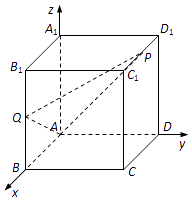
(1)若 ![]() ,求AP与AQ所成角的余弦值;
,求AP与AQ所成角的余弦值;
(2)若直线AA1与平面APQ所成的角为45°,求实数λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的首项为1,且
的首项为1,且![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,对任意
,对任意![]() ,都有
,都有![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() .若对任意的
.若对任意的![]() ,不等式
,不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx,(a∈R). (Ⅰ)当a=1时,求f(x)的单调区间;
(Ⅱ)若函数f(x)在(0, ![]() )上无零点,求a的取值范围.
)上无零点,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com