
【题目】已知数列![]() 的首项为1,且
的首项为1,且![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,对任意
,对任意![]() ,都有
,都有![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() .若对任意的
.若对任意的![]() ,不等式
,不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
试题(1)由![]() ,得
,得![]() ,又
,又![]() ,两式相减得
,两式相减得![]() ,整理得
,整理得![]() ,即
,即![]() ,又因为
,又因为![]() ,
,![]() ,
,
利用累积法得![]() ,
,
从而可求出数学![]() 的通项公式为
的通项公式为![]() ;
;
在数列![]() 中,由
中,由![]() ,得
,得![]() ,且
,且![]() ,
,
所以数学![]() 是以首项为
是以首项为![]() ,公比为
,公比为![]() 的等比数列,从而数列
的等比数列,从而数列![]() 的通项公式为
的通项公式为![]() .
.
(2)由题意得![]() ,
,
![]() ,
,
两式相减得![]()
![]() ,
,
由等比数列前![]() 项和公式可求得
项和公式可求得![]() ,
,
由不等式![]() 恒成立,得
恒成立,得![]() 恒成立,
恒成立,
即![]() (
(![]() )恒成立,
)恒成立,
构造函数![]() (
(![]() ),
),
当![]() 时,
时,![]() 恒成立,则
恒成立,则![]() 不满足条件;
不满足条件;
当![]() 时,由二次函数性质知不恒成立;
时,由二次函数性质知不恒成立;
当![]() 时,
时,![]() 恒成立,则
恒成立,则![]() 满足条件.
满足条件.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:(1)∵![]() ,∴
,∴![]() (
(![]() ),两式相减得,
),两式相减得,![]() ,
,
∴![]() ,即
,即![]() (
(![]() ),又因为
),又因为![]() ,
,![]() ,从而
,从而![]()
∴![]() (
(![]() ),
),
故数列![]() 的通项公式
的通项公式![]() (
(![]() ).
).
在数列![]() 中,由
中,由![]() ,知数列
,知数列![]() 是等比数列,首项、公比均为
是等比数列,首项、公比均为![]() ,
,
∴数列![]() 的通项公式
的通项公式![]() .
.
(2)∴![]() ①
①
∴![]() ②
②
由①-②,得![]()
![]() ,
,
∴![]() ,
,
不等式![]() 即为
即为![]() ,
,
即![]() (
(![]() )恒成立.
)恒成立.
方法一、设![]() (
(![]() ),
),
当![]() 时,
时,![]() 恒成立,则
恒成立,则![]() 不满足条件;
不满足条件;
当![]() 时,由二次函数性质知不恒成立;
时,由二次函数性质知不恒成立;
当![]() 时,
时,![]() 恒成立,则
恒成立,则![]() 满足条件.
满足条件.
综上所述,实数λ的取值范围是![]() .
.
方法二、也即![]() (
(![]() )恒成立,
)恒成立,
令![]() .则
.则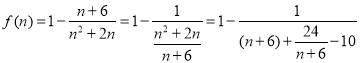 ,
,
由![]() ,
,![]() 单调递增且大于0,∴
单调递增且大于0,∴![]() 单调递增∴
单调递增∴![]()
∴实数λ的取值范围是![]() .
.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)是定义域为(0,+∞)的单调函数,若对任意的x∈(0,+∞),都有 ![]() ,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,则实数a的取值范围是( )
,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,则实数a的取值范围是( )
A.0<a≤5
B.a<5
C.0<a<5
D.a≥5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆 ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,焦点到相应准线的距离为1.
,焦点到相应准线的距离为1. 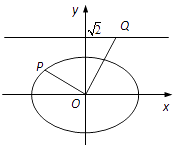
(1)求椭圆的标准方程;
(2)若P为椭圆上的一点,过点O作OP的垂线交直线 ![]() 于点Q,求
于点Q,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个同学分別抛掷一枚质地均匀的骰子.
(1)求他们抛掷的骰子向上的点数之和是4的倍数的概率;
(2)求甲抛掷的骰子向上的点数不大于乙抛掷的骰子向上的点数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海南沿海某次超强台风过后,当地人民积极恢复生产,焊接工王师傅每天都很忙碌.一天他遇到了一个难题:如图所示,有一块扇形钢板,半径为![]() 米,圆心角
米,圆心角![]() ,施工要求按图中所画的那样,在钢板
,施工要求按图中所画的那样,在钢板![]() 上裁下一块平行四边形钢板
上裁下一块平行四边形钢板![]() ,要求使裁下的钢板面积最大.请你帮助王师傅解决此问题.连接
,要求使裁下的钢板面积最大.请你帮助王师傅解决此问题.连接![]() ,设
,设![]() ,过
,过![]() 作
作![]() ,垂足为
,垂足为![]() .
.

(1)求线段![]() 的长度(用
的长度(用![]() 来表示);
来表示);
(2)求平行四边形![]() 面积的表达式(用
面积的表达式(用![]() 来表示);
来表示);
(3)为使平行四边形![]() 面积最大,
面积最大,![]() 等于何值?最大面积是多少?
等于何值?最大面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() (侧棱垂直于底面)中,
(侧棱垂直于底面)中,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,在线段
的中点,在线段![]() 上是否存在一点
上是否存在一点![]() 使
使![]() 平面
平面![]() ?若存在,请确定点
?若存在,请确定点![]() 的位置;若不存在,也请说明理由.
的位置;若不存在,也请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划.![]() 年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本
年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本![]() 万元,每生产
万元,每生产![]() (百辆),需另投入成本
(百辆),需另投入成本![]() 万元,且
万元,且 .由市场调研知,每辆车售价
.由市场调研知,每辆车售价![]() 万元,且全年内生产的车辆当年能全部销售完.
万元,且全年内生产的车辆当年能全部销售完.
(1)求出2018年的利润![]() (万元)关于年产量
(万元)关于年产量![]() (百辆)的函数关系式;(利润=销售额-成本)
(百辆)的函数关系式;(利润=销售额-成本)
(2)2018年产量为多少百辆时,企业所获利润最大?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com