
����Ŀ�������غ�ij�γ�ǿ̨���������������ָ����������ӹ���ʦ��ÿ�춼��æµ��һ����������һ�����⣺��ͼ��ʾ����һ�����θְ壬�뾶Ϊ![]() �ף�Բ�Ľ�
�ף�Բ�Ľ�![]() ��ʩ��Ҫ��ͼ���������������ڸְ�
��ʩ��Ҫ��ͼ���������������ڸְ�![]() �ϲ���һ��ƽ���ı��θְ�
�ϲ���һ��ƽ���ı��θְ�![]() ��Ҫ��ʹ���µĸְ����������������ʦ����������⣮����
��Ҫ��ʹ���µĸְ����������������ʦ����������⣮����![]() ����
����![]() ����
����![]() ��
��![]() ������Ϊ
������Ϊ![]() .
.

��1�����߶�![]() �ij��ȣ���
�ij��ȣ���![]() ����ʾ����
����ʾ����
��2����ƽ���ı���![]() ����ı���ʽ����
����ı���ʽ����![]() ����ʾ����
����ʾ����
��3��Ϊʹƽ���ı���![]() ������
������![]() ���ں�ֵ���������Ƕ��٣�
���ں�ֵ���������Ƕ��٣�
���𰸡���1��![]() ��2��
��2��![]() ��3����
��3����![]() ʱ�����øְ��������������Ϊ
ʱ�����øְ��������������Ϊ![]() ƽ���ף�
ƽ���ף�
��������
��1���ȸ���������![]() �б�ʾ
�б�ʾ![]() ������
������![]() �б�ʾ
�б�ʾ![]() ����.
����.
��2���ɣ�1��֪![]() ��
��![]() �� ��
�� ��![]() ��֪
��֪![]() ����ʾƽ���ı������
����ʾƽ���ı������![]() ����϶����ǹ�ʽ���������Ǻ͵����ҹ�ʽ��ʾ����.
����϶����ǹ�ʽ���������Ǻ͵����ҹ�ʽ��ʾ����.
��3���ɣ�2�����![]() �����������ֵ����.
�����������ֵ����.
�⣺��1����![]() �У�
��![]() ��
��![]() ��
��
![]() �ı���
�ı���![]() Ϊƽ���ı���
Ϊƽ���ı���![]() ��
��![]() ��
��![]()
��![]() ��
��![]()
����![]() ��
��
��2��![]() ��
��
��ƽ���ı���![]() �����Ϊ
�����Ϊ![]() ��
��
��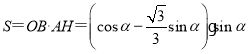
��![]()
��![]()
��![]()
��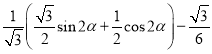
��![]() ��
��
��3������![]() ��
��
����![]() ��
��
��![]() ����
����![]() ʱ��
ʱ��
![]() ��
��
���Ե�![]() ʱ�����øְ��������������Ϊ
ʱ�����øְ��������������Ϊ![]() ƽ���ף�
ƽ���ף�


 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() .
.
��1����ֱ��![]() ������
������![]() ������Բ
������Բ![]() ���У���
���У���![]() �ķ��̣�
�ķ��̣�
��2����Բ![]() �İ뾶Ϊ
�İ뾶Ϊ![]() ��Բ����ֱ��
��Բ����ֱ��![]() �ϣ�����Բ
�ϣ�����Բ![]() ���У���Բ
���У���Բ![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˲μ�ij�˶���,����֧��ǿ���������ѡ��18�����Ů��������Ҷ�,��Ա��Դ�������±�:
�ӱ� | ���� | �Ϻ� | ��� | ��һ |
���� | 4 | 6 | 3 | 5 |
(1)����18����Ա�����ѡ������,����������ͬһ�ӵĸ���;
(2)��Ҫ��ѡ��������Ա���������ӳ�,���������Ա����ӵ�����Ϊ![]() ,���������
,���������![]() �ķֲ���.
�ķֲ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ⳤΪ2��������ABCD��A1B1C1D1�У�PΪ��C1D1���е㣬QΪ��BB1�ϵĵ㣬��BQ=��BB1���ˡ�0���� 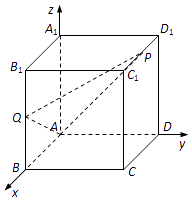
��1���� ![]() ����AP��AQ���ɽǵ�����ֵ��
����AP��AQ���ɽǵ�����ֵ��
��2����ֱ��AA1��ƽ��APQ���ɵĽ�Ϊ45�㣬��ʵ���˵�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ե�![]() ΪԲ�ĵ�Բ
ΪԲ�ĵ�Բ![]() ��ֱ��
��ֱ��![]() ��
��![]() �صõ��ҳ�Ϊ
�صõ��ҳ�Ϊ![]() .
.
��1����Բ![]() �ı����̣�
�ı����̣�
��2�����![]() ��Բ
��Բ![]() ���е�ֱ�߷��̣�
���е�ֱ�߷��̣�
��3����![]() ��
��![]() ��Ķ��㣬
��Ķ��㣬![]() ��
��![]() �ֱ���Բ
�ֱ���Բ![]() ��
��![]() ��
��![]() ����.���ʣ�ֱ��
����.���ʣ�ֱ��![]() �Ƿ������㣿���ǣ������������ꣻ�����ǣ�˵������.
�Ƿ������㣿���ǣ������������ꣻ�����ǣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������Ϊ1����
������Ϊ1����![]() ������
������![]() ����
����![]() ��
��![]() ��������
��������![]() ������
������![]() .
.
��1��������![]() ��
��![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2����![]() ������
������![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() .���������
.���������![]() ������ʽ
������ʽ![]() �����������ʵ��
�����������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݹ��һ����������ġ������������������涨��������PM2.5����ƽ��Ũ�Ȳ��ó���35��/�����ף�PM2.5��24Сʱƽ��Ũ�Ȳ��ó���75��/�����ף����л����������ȡ��һ������2016��20��PM2.5��24Сʱƽ��Ũ�ȣ���λ����/�����ף��ļ�����ݣ�����ͳ�������
��� | PM2.5Ũ�� | Ƶ�����죩 | Ƶ�� |
��һ�� | ��0��25] | 3 | 0.15 |
�ڶ��� | ��25��50] | 12 | 0.6 |
������ | ��50��75] | 3 | 0.15 |
������ | ��75��100] | 2 | 0.1 |
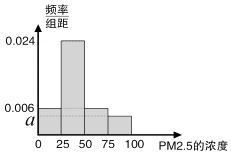
��1������20��IJ���������ϱ��з��鷽�����Ƴɵ�����Ƶ�ʷֲ�ֱ��ͼ��ͼ�� ����ͼ4��a��ֵ��
��������ƽ�������������������������˼�룬��PM2.5����ƽ��Ũ�ȿ��ǣ��жϸþ������Ļ��������Ƿ���Ҫ���ƣ���˵�����ɣ�
��2����Ƶ����Ϊ���ʣ�����2016���ij3�죬����3���иþ�����PM2.5��24Сʱƽ��Ũ�ȷ��ϻ�������������������ΪX����X�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����![]() �ı����Ϊ
�ı����Ϊ![]() ������
������![]() Ϊ�ռ�ֱ������ϵ
Ϊ�ռ�ֱ������ϵ![]() ��ԭ�㣬����
��ԭ�㣬����![]() �ֱ���
�ֱ���![]() ����������ύ��
����������ύ��![]() ���㣬��֪������һ��
���㣬��֪������һ��![]() .
.
��1����![]() ��������
��������![]() �ϵ�������룻
�ϵ�������룻
��2������![]() ��ƽ��
��ƽ��![]() �Ĵ��ߣ�����
�Ĵ��ߣ�����![]() ����
����![]() �����꣬������������
�����꣬������������![]() �������
�������
��3����ƽ��![]() ��ƽ��
��ƽ��![]() ���������ǵĴ�С.
���������ǵĴ�С.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������12�֣�һ��������װ�����ſ�Ƭ���ֱ���������![]() ��
��![]() ��
��![]() �������ſ�Ƭ����ǵ���������ȫ��ͬ������зŻصس�ȡ
�������ſ�Ƭ����ǵ���������ȫ��ͬ������зŻصس�ȡ![]() �Σ�ÿ�γ�ȡ
�Σ�ÿ�γ�ȡ![]() �ţ�����ȡ�Ŀ�Ƭ�ϵ��������μ�Ϊ
�ţ�����ȡ�Ŀ�Ƭ�ϵ��������μ�Ϊ![]() ��
��![]() ��
��![]() .
.
������������ȡ�Ŀ�Ƭ�ϵ���������![]() ���ĸ��ʣ�
���ĸ��ʣ�
������������ȡ�Ŀ�Ƭ�ϵ�����![]() ��
��![]() ��
��![]() ����ȫ��ͬ���ĸ���.
����ȫ��ͬ���ĸ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com