
函数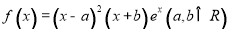 .
.
(I)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(II)若 是
是 的极大值点.
的极大值点.
(i)当 时,求
时,求 的取值范围;
的取值范围;
(ii)当 为定值时,设
为定值时,设 是
是 的3个极值点,问:是否存在实数
的3个极值点,问:是否存在实数 ,可找到
,可找到 使得
使得 的某种排列成等差数列?若存在,求出所有的
的某种排列成等差数列?若存在,求出所有的 的值及相应的
的值及相应的 ;若不存在,说明理由.
;若不存在,说明理由.
科目:高中数学 来源:2016届江西省九江市高三下学期三模理科数学试卷(解析版) 题型:选择题
复数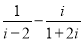 在复平面内所对应的点位于( )
在复平面内所对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:高中数学 来源:2016届云南省高三适应性月考八理科数学试卷(解析版) 题型:选择题
已知 为正实数,则
为正实数,则 是
是 的( )
的( )
A.充分不必要条件 B.必要不充分条件
C.既不充分也不必要条件 D.充分必要条件
查看答案和解析>>
科目:高中数学 来源:2016届西藏日喀则一中高三下学期二模文科数学试卷(解析版) 题型:选择题
如图,在正方体 中
中 分别为棱
分别为棱 的中点,用过点
的中点,用过点 的平面截去该正方体的上半部分,则剩余几何体(下半部分)的左视图为( )
的平面截去该正方体的上半部分,则剩余几何体(下半部分)的左视图为( )


查看答案和解析>>
科目:高中数学 来源:2016届西藏日喀则一中高三下学期二模理科数学试卷(解析版) 题型:解答题
已知函数 在
在 处取得最值,其中
处取得最值,其中 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)将函数 的图象向左平移
的图象向左平移 个单位,再将所得图象上各点的横坐标伸长为原来的3倍,纵坐标不变,得到函数
个单位,再将所得图象上各点的横坐标伸长为原来的3倍,纵坐标不变,得到函数 的图象,若
的图象,若 为锐角,
为锐角, ,求
,求 .
.
查看答案和解析>>
科目:高中数学 来源:2016届江苏省高三考前一周双练三模数学试卷(解析版) 题型:解答题
某商场为促销要准备一些正三棱锥形状的装饰品,用半径为
 的圆形包装纸包装.要求如下:正三棱锥的底面中心与包装纸的圆心重合,包装纸不能裁剪,沿底边向上翻折,其边缘恰好达到三棱锥的顶点,如图所示.设正三棱锥的底面边长为
的圆形包装纸包装.要求如下:正三棱锥的底面中心与包装纸的圆心重合,包装纸不能裁剪,沿底边向上翻折,其边缘恰好达到三棱锥的顶点,如图所示.设正三棱锥的底面边长为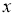
 ,体积为
,体积为
 .
.

(1)求 关于
关于 的函数关系式;
的函数关系式;
(2)在所有能用这种包装纸包装的正三棱锥装饰品中, 的最大值是多少?并求此时
的最大值是多少?并求此时 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2016届四川省高三下三诊考试理科数学试卷(解析版) 题型:解答题
已知各项均为正数的数列 的前
的前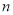 项
项 满足
满足 .
.
(1)求数列 通项公式;
通项公式;
(2)设 为数列
为数列 的前
的前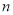 项和,若
项和,若 对
对 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com