
【题目】如图,四棱锥![]() 中,二面角
中,二面角![]() 为直二面角,
为直二面角,![]() 为线段
为线段![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
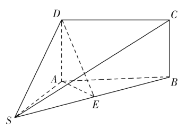
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
【答案】(1)证明见解析 (2)![]()
【解析】
(1)利用面面垂直的判定定理和性质定理及线面垂直的判定定理即可证明;
(2)连接![]() ,在平面
,在平面![]() 内作
内作![]() 的垂线,建立空间直角坐标系
的垂线,建立空间直角坐标系![]() 如图所示,
如图所示,
由(1)知![]() 为平面
为平面![]() 的一个法向量,设平面
的一个法向量,设平面![]() 的法向量为
的法向量为![]() ,根据题意,求出向量
,根据题意,求出向量![]() ,利用空间向量法求二面角的方法,则向量
,利用空间向量法求二面角的方法,则向量![]() 的夹角或其补角即为所求.
的夹角或其补角即为所求.
(1)证明![]() 二面角
二面角![]() 为直二面角,
为直二面角,
所以平面![]() 平面
平面![]() ,
,
因为![]() ,
,![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
又![]() 为
为![]() 的中点,
的中点,![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
(2)如图,
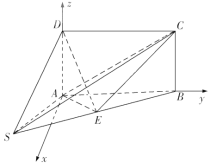
连接![]() ,在平面
,在平面![]() 内作
内作![]() 的垂线,建立空间直角坐标系
的垂线,建立空间直角坐标系![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
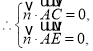 即
即 令
令![]() ,则
,则![]() ,
,![]() ,
,
![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() 的一个法向量为
的一个法向量为![]() ,
,
 ,
,
由图可知二面角![]() 的平面角为锐角,
的平面角为锐角,
故二面角![]() 的大小为
的大小为![]() .
.


科目:高中数学 来源: 题型:
【题目】某学校为了了解高一年级学生学习数学的状态,从期中考试成绩中随机抽取50名学生的数学成绩,按成绩分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
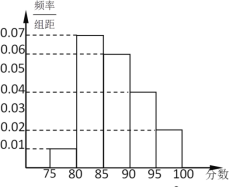
(1)由频率分布直方图,估计这50名学生数学成绩的中位数和平均数(保留到0.01);
(2)该校高一年级共有1000名学生,若本次考试成绩90分以上(含90分)为“优秀”等次,则根据频率分布直方图估计该校高一学生数学成绩达到“优秀”等次的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,北京2022年冬奥组委会启动志愿者全球招募,仅一个月内报名人数便突破60万,其中青年学生约有50万人.现从这50万青年学生志愿者中,按男女分层抽样随机选取20人进行英语水平测试,所得成绩(单位:分)统计结果用茎叶图记录如下:
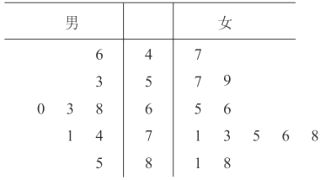
(Ⅰ)试估计在这50万青年学生志愿者中,英语测试成绩在80分以上的女生人数;
(Ⅱ)从选出的8名男生中随机抽取2人,记其中测试成绩在70分以上的人数为X,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)为便于联络,现将所有的青年学生志愿者随机分成若干组(每组人数不少于5000),并在每组中随机选取![]() 个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出
个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出![]() 的最小值.(结论不要求证明)
的最小值.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() 为
为![]() 中点,下列说法中
中点,下列说法中
(1)![]() ;
;
(2)记二面角![]() 的平面角分别为
的平面角分别为![]() ;
;
(3)记![]() 的面积分别为
的面积分别为![]() ;
;
(4)![]() ,
,
正确说法的个数为( )

A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ?如果存在,求
?如果存在,求![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() )上的两个动点
)上的两个动点![]() 和
和![]() ,焦点为F.线段
,焦点为F.线段![]() 的中点为
的中点为![]() ,且点到抛物线的焦点F的距离之和为8
,且点到抛物线的焦点F的距离之和为8
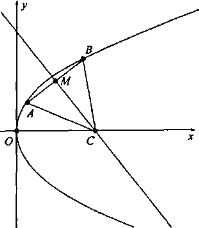
(1)求抛物线的标准方程;
(2)若线段![]() 的垂直平分线与x轴交于点C,求
的垂直平分线与x轴交于点C,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com