
分析 (1)根据题意直接可得结论;
(2)考查符合条件的数列P中,存在某个i(i≤i≤19)满足ai≤ai+1,通过Tk(P)=min{n|an≥k}(k∈N*),可得Tai+1(P)=i+1,故只需将数列P略作调整,仅将第ai的值增加1,即调整后s′=s.如果数列{an′}还有存在相邻两项不相等,继续做以上的操作,最终一定可以经过有限次的操作,使得{an}中的每一项变为相等,且操作中保持s的值不变,计算即可.
解答 解:(1)∵数列P:1?3?4?7?…,即从第三项起每项是前两项的和,
∴T1(P)=1,T2(P)=2,T3(P)=2,T4(P)=3,T5(P)=4;
故答案是:4;
(2)考查符合条件的数列P中,
若存在某个i(1≤i≤19)满足ai≤ai+1,
对应可得Tk(P),及s=a1+a2+…+a20+T1(P)+T2(P)+…+T46(P).
∵Tk(P)=min{n|an≥k}(k∈N*),∴Tai+1(P)=i+1,
下面将数列P略作调整,仅将第ai的值增加1,具体如下:
将aj′=aj+1,对于任何j(j≠1)令aj′=aj,可得数列P′及其对应数列Tk(P′),
根据数列Tk(P′)的定义,可得Tai+1(P′)=i,且Tj(P′)=Tj(P)(j≠ai+1).
显然Tai+1(P′)=Tai+1(P)-1,
∴s′=a1′+a2′+…+a20′+T1(P′)+T2(P′)+…+T46(P′)
=a1+a2+…+ai-1+(ai+1)+ai+1+…+a20+T1(P)+T2(P)+…+(Tai+1-1)+Tai+2+…+T46(P)
=a1+a2+…+a20+T1(P)+T2(P)+…+T46(P)=s,
即调整后s′=s.
如果数列{an′}还有存在相邻两项不相等,继续做以上的操作,
最终一定可以经过有限次的操作,使得{an}中的每一项变为相等,
且操作中保持s的值不变,
而当a1=a2=…=a20=46时,T1(P)=T2(P)=…=T46(P)=1,
∴s=a1+a2+…+a20+T1(P)+T2(P)+…+T46(P)=46×20+46=966.
故答案是:966.
点评 本题是一道建立在数列上的新定义题,考查分类讨论的思想,考查分析问题、解决问题的能力,属于难题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 3lg2 | B. | 2lg2 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
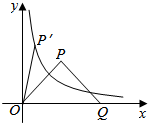 已知函数f(x)=asin($\frac{π}{4}$x)(a>0)在同一半周期内的图象过点O,P,Q,其中O为坐标原点,P为函数f(x)的最高点,Q为函数f(x)的图象与x轴的正半轴的交点,△OPQ为等腰直角三角形.
已知函数f(x)=asin($\frac{π}{4}$x)(a>0)在同一半周期内的图象过点O,P,Q,其中O为坐标原点,P为函数f(x)的最高点,Q为函数f(x)的图象与x轴的正半轴的交点,△OPQ为等腰直角三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com