
分析 通过a12+a22+…an2=$\frac{{4}^{n}-1}{3}$与a12+a22+…an2+${{a}_{n+1}}^{2}$=$\frac{{4}^{n+1}-1}{3}$作差,整理可得当n≥2时an=2n-1,进而an=2n-1,计算即得结论.
解答 解:∵a12+a22+…an2=$\frac{{4}^{n}-1}{3}$,
∴a12+a22+…an2+${{a}_{n+1}}^{2}$=$\frac{{4}^{n+1}-1}{3}$,
两式相减得:${{a}_{n+1}}^{2}$=$\frac{{4}^{n+1}-1}{3}$-$\frac{{4}^{n}-1}{3}$=4n=22n,
又∵an>0,
∴an+1=2n=2(n+1)-1,
∴当n≥2时,an=2n-1,
又∵a12=$\frac{4-1}{3}$=1,即a1=1,满足上式,
∴an=2n-1,
∴Sn=$\frac{1-{2}^{n}}{1-2}$=2n-1.
点评 本题考查数列的通项及前n项和,考查运算求解能力,分析问题、解决问题的能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
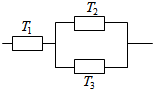 三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2}\;,\frac{3}{4}\;,\frac{3}{4}$,将它们中某两个元件并联后再和第三个元件串联接入电路.
三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2}\;,\frac{3}{4}\;,\frac{3}{4}$,将它们中某两个元件并联后再和第三个元件串联接入电路.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com