
【题目】针对国家提出的延迟退休方案,某机构进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| 支持 | 保留 | 不支持 |
|
|
|
|
|
|
|
|
(1)在所有参与调查的人中,用分层抽样的方法抽取![]() 个人,已知从持“不支持”态度的人中抽取了
个人,已知从持“不支持”态度的人中抽取了![]() 人,求
人,求![]() 的值;
的值;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取![]() 人看成一个总体,从这
人看成一个总体,从这![]() 人中任意选取
人中任意选取![]() 人,求
人,求![]() 岁以下人数
岁以下人数![]() 的分布列和期望;
的分布列和期望;
(3)在接受调查的人中,有![]() 人给这项活动打出的分数如下:
人给这项活动打出的分数如下: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,把这
,把这![]() 个人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过
个人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过![]() 概率.
概率.
【答案】(1)![]() ;(2)分布列见解析,
;(2)分布列见解析, ![]() ;(3)
;(3)![]() .
.
【解析】试题分析:
(1)由题意可知参与调查的总人数为![]() ,结合分层抽样的概念计算可得
,结合分层抽样的概念计算可得![]() .
.
(2)由题意可知抽取的![]() 人中,
人中, ![]() 岁以下与
岁以下与![]() 岁以上人数分别为
岁以上人数分别为![]() 人,
人, ![]() 人,则
人,则![]() ,计算相应的概率值有
,计算相应的概率值有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,据此可得分布列,计算相应的期望为
,据此可得分布列,计算相应的期望为![]() .
.
(3)总体的平均数为![]() ,则与总体平均数之差的绝对值超过
,则与总体平均数之差的绝对值超过![]() 的数有
的数有![]() ,
, ![]() ,
, ![]() ,由古典概型计算公式可得满足题意的概率值为
,由古典概型计算公式可得满足题意的概率值为![]() .
.
试题解析:
(1)参与调查的总人数为![]() ,其中从持“不支持”态度的人数
,其中从持“不支持”态度的人数![]() 中抽取了
中抽取了![]() 人,所以
人,所以![]() .
.
(2)在持“不支持”态度的人中, ![]() 岁以下及
岁以下及![]() 岁以上人数之比为
岁以上人数之比为![]() ,因此抽取的
,因此抽取的![]() 人中,
人中, ![]() 岁以下与
岁以下与![]() 岁以上人数分别为
岁以上人数分别为![]() 人,
人, ![]() 人,
人, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
|
|
|
|
|
|
|
|
|
|
![]() .
.
(3)总体的平均数为![]()
![]() ,
,
那么与总体平均数之差的绝对值超过![]() 的数有
的数有![]() ,
, ![]() ,
, ![]() ,所以任取
,所以任取![]() 个数与总体平均数之差的绝对值超过
个数与总体平均数之差的绝对值超过![]() 的概率为
的概率为![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】某市交通管理有关部门对![]() 年参加驾照考试的
年参加驾照考试的![]() 岁以下的学员随机抽取
岁以下的学员随机抽取![]() 名学员,对他们的科目三(道路驾驶)和科目四(安全文明相关知识)进行两轮测试,并把两轮成绩的平均分作为该学员的抽测成绩,记录数据如下:
名学员,对他们的科目三(道路驾驶)和科目四(安全文明相关知识)进行两轮测试,并把两轮成绩的平均分作为该学员的抽测成绩,记录数据如下:
学员编号 |
|
|
|
|
|
|
|
|
|
|
科目三成绩 |
|
|
|
|
|
|
|
|
|
|
科目四成绩 |
|
|
|
|
|
|
|
|
|
|
(1)从![]() 年参加驾照考试的
年参加驾照考试的![]() 岁以下学员中随机抽取一名学员,估计这名学员抽测成绩大于或等于
岁以下学员中随机抽取一名学员,估计这名学员抽测成绩大于或等于![]() 分的概率;
分的概率;
(2)根据规定,科目三和科目四测试成绩均达到![]() 分以上(含
分以上(含![]() 分)才算合格,从抽测的
分)才算合格,从抽测的![]() 到
到![]() 号学员中任意抽取两名学员,记
号学员中任意抽取两名学员,记![]() 为抽取学员不合格的人数,求
为抽取学员不合格的人数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小组为了研究昼夜温差对一种稻谷种子发芽情况的影响,他们分别记录了4月1日至4月5日的每天星夜温差与实验室每天每100颗种子的发芽数,得到如下资料:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
温差 | 9 | 10 | 11 | 8 | 12 |
发芽数 | 38 | 30 | 24 | 41 | 17 |
利用散点图,可知![]() 线性相关。
线性相关。
(1)求出![]() 关于
关于![]() 的线性回归方程,若4月6日星夜温差
的线性回归方程,若4月6日星夜温差![]() ,请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数;
,请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数;
(2)若从4月1日![]() 4月5日的五组实验数据中选取2组数据,求这两组恰好是不相邻两天数据的概率.
4月5日的五组实验数据中选取2组数据,求这两组恰好是不相邻两天数据的概率.
(公式: )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .将
.将![]() 的图象向左平移
的图象向左平移![]() 个单位长度后所得的函数为偶函数,则关于函数
个单位长度后所得的函数为偶函数,则关于函数![]() ,下列命题正确的是( )
,下列命题正确的是( )
A. 函数![]() 在区间
在区间![]() 上有最小值 B. 函数
上有最小值 B. 函数![]() 在区间
在区间![]() 上单调递增
上单调递增
C. 函数![]() 的一条对称轴为
的一条对称轴为![]() D. 函数
D. 函数![]() 的一个对称点为
的一个对称点为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学利用暑假时间到一家商场勤工俭学,该商场向他提供了三种付酬方案:
第一种,每天支付![]() 元,没有奖金;
元,没有奖金;
第二种,每天的底薪![]() 元,另有奖金.第一天奖金
元,另有奖金.第一天奖金![]() 元,以后每天支付的薪酬中奖金比前一天的奖金多
元,以后每天支付的薪酬中奖金比前一天的奖金多![]() 元;
元;
第三种,每天无底薪,只有奖金.第一天奖金![]() 元,以后每天支付的奖金是前一天的奖金的
元,以后每天支付的奖金是前一天的奖金的![]() 倍.
倍.
(1)工作![]() 天
天![]() ,记三种付费方式薪酬总金额依次为
,记三种付费方式薪酬总金额依次为![]() 、
、![]() 、
、![]() ,写出
,写出![]() 、
、![]() 、
、![]() 关于
关于![]() 的表达式;
的表达式;
(2)该学生在暑假期间共工作![]() 天,他会选择哪种付酬方式?
天,他会选择哪种付酬方式?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,(CUA)∩B;
(2)若A∩C≠![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数:f(x)=x2﹣mx﹣n(m, n∈R).
(1)若m+n=0,解关于x的不等式f(x)≥x(结果用含m式子表示);
(2)若存在实数m,使得当x∈[1,2]时,不等式x≤f(x)≤4x恒成立,求实数n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全国第五个“扶贫日”到来之前,某省开展“精准扶贫,携手同行”的主题活动,某贫困县调查基层干部走访贫困户数量.![]() 镇有基层干部60人,
镇有基层干部60人,![]() 镇有基层干部60人,
镇有基层干部60人,![]() 镇有基层干部80人,每人都走访了若干贫困户,按照分层抽样,从
镇有基层干部80人,每人都走访了若干贫困户,按照分层抽样,从![]() 三镇共选40名基层干部,统计他们走访贫困户的数量,并将走访数量分成5组,
三镇共选40名基层干部,统计他们走访贫困户的数量,并将走访数量分成5组,![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
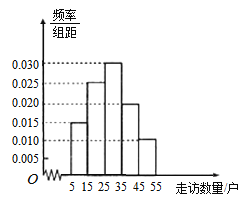
(1)求这40人中有多少人来自![]() 镇,并估计
镇,并估计![]() 三镇的基层干部平均每人走访多少贫困户;(同一组中的数据用该组区间的中点值作代表)
三镇的基层干部平均每人走访多少贫困户;(同一组中的数据用该组区间的中点值作代表)
(2)如果把走访贫困户达到或超过25户视为工作出色,以频率估计概率,从![]() 三镇的所有基层干部中随机选取3人,记这3人中工作出色的人数为
三镇的所有基层干部中随机选取3人,记这3人中工作出色的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com