
【题目】如图,四棱锥![]() 中,四边形
中,四边形![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() 为正三角形,且平面
为正三角形,且平面![]() 平面
平面![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)求几何体![]() 的体积.
的体积.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】现准备将8本相同的书全部分配给5个不同的班级,其中甲、乙两个班级每个班级至少2本,其它班级允许1本也没有,则不同的分配方案共有( )
A.60种B.70种C.82种D.92种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】绿色已成为当今世界主题,绿色动力已成为时代的驱动力,绿色能源是未来新能源行业的主导.某汽车公司顺应时代潮流,最新研发了一款新能源汽车,并在出厂前对100辆汽车进行了单次最大续航里程(理论上是指新能源汽车所装载的燃料或电池所能够提供给车行驶的最远里程)的测试.现对测试数据进行分析,得到如图所示的频率分布直方图.
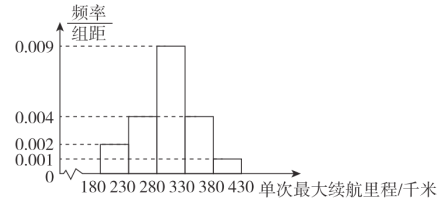
(1)估计这100辆汽车的单次最大续航里程的平均值![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)根据大量的汽车测试数据,可以认为这款汽车的单次最大续航里程![]() 近似地服从正态分布
近似地服从正态分布![]() ,经计算第(1)问中样本标准差
,经计算第(1)问中样本标准差![]() 的近似值为50.用样本平均数
的近似值为50.用样本平均数![]() 作为
作为![]() 的近似值,用样本标准差
的近似值,用样本标准差![]() 作为
作为![]() 的估计值;
的估计值;
(ⅰ)现从该汽车公司最新研发的新能源汽车中任取一辆汽车,求它的单次最大续航里程恰好在200千米到350千米之间的概率;
(ⅱ)从该汽车公司最新研发的新能源汽车中随机抽取10辆,设这10辆汽车中单次最大续航里程恰好在200千米到350千米之间的数量为![]() ,求
,求![]() ;
;
(3)某汽车销售公司为推广此款新能源汽车,现面向意向客户推出“玩游戏,送大奖”活动,客户可根据抛掷硬币的结果,操控微型遥控车在方格图上行进,若遥控车最终停在“胜利大本营”,则可获得购车优惠券.已知硬币出现正、反面的概率都是![]() ,方格图上标有第0格、第1格、第2格、…、第50格.遥控车开始在第0格,客户每掷一次硬币,遥控车向前移动一次,若掷出正面,遥控车向前移动一格(从
,方格图上标有第0格、第1格、第2格、…、第50格.遥控车开始在第0格,客户每掷一次硬币,遥控车向前移动一次,若掷出正面,遥控车向前移动一格(从![]() 到
到![]() ),若掷出反面,遥控车向前移动两格(从
),若掷出反面,遥控车向前移动两格(从![]() 到
到![]() ),直到遥控车移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束.设遥控车移到第
),直到遥控车移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束.设遥控车移到第![]() 格的概率为
格的概率为![]() ,其中
,其中![]() ,试说明
,试说明![]() 是等比数列,并解释此方案能否成功吸引顾客购买该款新能源汽车.
是等比数列,并解释此方案能否成功吸引顾客购买该款新能源汽车.
参考数据:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】松、竹、梅经冬不衰,因此有“岁寒三友”之称.在我国古代的诗词和典籍中有很多与松和竹相关的描述和记载,宋代刘学箕的《念奴娇·水轩沙岸》的“缀松黏竹,恍然如对三绝”描写了大雪后松竹并生相依的美景;宋元时期数学名著《算学启蒙》中亦有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.现欲知几日后,竹长超过松长一倍.为了解决这个新问题,设计下面的程序框图,若输入的![]() ,
,![]() ,则输出的
,则输出的![]() 的值为( )
的值为( )
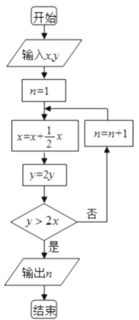
A.4B.5C.6D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国2019年新年贺岁大片《流浪地球》自上映以来引发了社会的广泛关注,受到了观众的普遍好评.假设男性观众认为《流浪地球》好看的概率为![]() ,女性观众认为《流浪地球》好看的概率为
,女性观众认为《流浪地球》好看的概率为![]() ,某机构就《流浪地球》是否好看的问题随机采访了4名观众(其中2男2女).
,某机构就《流浪地球》是否好看的问题随机采访了4名观众(其中2男2女).
(1)求这4名观众中女性认为好看的人数比男性认为好看的人数多的概率;
(2)设![]() 表示这4名观众中认为《流浪地球》好看的人数,求
表示这4名观众中认为《流浪地球》好看的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() 为
为![]() 的导函数,且
的导函数,且![]() .
.
(1)求实数![]() 的值;
的值;
(2)若函数![]() 在
在![]() 处的切线经过点
处的切线经过点![]() ,求函数
,求函数![]() 的极值;
的极值;
(3)若关于![]() 的不等式
的不等式![]() 对于任意的
对于任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有4名同学去参加校学生会活动,共有甲、乙两类活动可供参加者选择,为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪类活动,掷出点数为1或2的人去参加甲类活动,掷出点数大于2的人去参加乙类活动.
(1)求这4个人中恰有2人去参加甲类活动的概率;
(2)用![]() ,
,![]() 分别表示这4个人中去参加甲、乙两类活动的人数.记
分别表示这4个人中去参加甲、乙两类活动的人数.记![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两个班级均为 40 人,进行一门考试后,按学生考试成绩及格与不及格进行统计,甲班及格人数为 36 人,乙班及格人数为 24 人.
(1)根据以上数据建立一个2![]() 2的列联表;
2的列联表;
(2)试判断是否成绩与班级是否有关?
参考公式:![]() ;
;![]()
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com