
ΓΨΧβΡΩΓΩ¬Χ…Ϊ“―≥…ΈΣΒ±Ϋώ άΫγ÷ςΧβΘ§¬Χ…ΪΕ·ΝΠ“―≥…ΈΣ ±¥ζΒΡ«ΐΕ·ΝΠΘ§¬Χ…ΪΡή‘¥ «Έ¥ά¥–¬Ρή‘¥––“ΒΒΡ÷ςΒΦΘ°Ρ≥Τϊ≥ΒΙΪΥΨΥ≥”Π ±¥ζ≥±ΝςΘ§Ήν–¬―–ΖΔΝΥ“ΜΩν–¬Ρή‘¥Τϊ≥ΒΘ§≤Δ‘Ύ≥ω≥ß«ΑΕ‘100ΝΨΤϊ≥ΒΫχ––ΝΥΒΞ¥ΈΉν¥σ–χΚΫάο≥ΧΘ®άμ¬έ…œ «÷Η–¬Ρή‘¥Τϊ≥ΒΥυΉΑ‘ΊΒΡ»ΦΝœΜρΒγ≥ΊΥυΡήΙΜΧαΙ©Ηχ≥Β–– ΜΒΡΉν‘Εάο≥ΧΘ©ΒΡ≤β ‘Θ°œ÷Ε‘≤β ‘ ΐΨίΫχ––Ζ÷ΈωΘ§ΒΟΒΫ»γΆΦΥυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ°
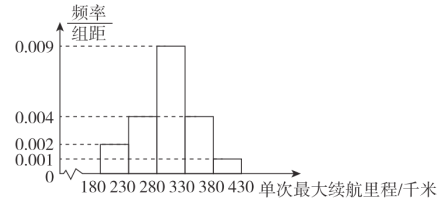
Θ®1Θ©ΙάΦΤ’β100ΝΨΤϊ≥ΒΒΡΒΞ¥ΈΉν¥σ–χΚΫάο≥ΧΒΡΤΫΨυ÷Β![]() Θ®Ά§“ΜΉι÷–ΒΡ ΐΨί”ΟΗΟΉι«χΦδΒΡ÷–Βψ÷Β¥ζ±μΘ©ΘΜ
Θ®Ά§“ΜΉι÷–ΒΡ ΐΨί”ΟΗΟΉι«χΦδΒΡ÷–Βψ÷Β¥ζ±μΘ©ΘΜ
Θ®2Θ©ΗυΨί¥σΝΩΒΡΤϊ≥Β≤β ‘ ΐΨίΘ§Ω…“‘»œΈΣ’βΩνΤϊ≥ΒΒΡΒΞ¥ΈΉν¥σ–χΚΫάο≥Χ![]() ΫϋΥΤΒΊΖΰ¥”’ΐΧ§Ζ÷≤Φ
ΫϋΥΤΒΊΖΰ¥”’ΐΧ§Ζ÷≤Φ![]() Θ§Ψ≠ΦΤΥψΒΎΘ®1Θ©Έ ÷–―υ±Ψ±ξΉΦ≤ν
Θ§Ψ≠ΦΤΥψΒΎΘ®1Θ©Έ ÷–―υ±Ψ±ξΉΦ≤ν![]() ΒΡΫϋΥΤ÷ΒΈΣ50Θ°”Ο―υ±ΨΤΫΨυ ΐ
ΒΡΫϋΥΤ÷ΒΈΣ50Θ°”Ο―υ±ΨΤΫΨυ ΐ![]() ΉςΈΣ
ΉςΈΣ![]() ΒΡΫϋΥΤ÷ΒΘ§”Ο―υ±Ψ±ξΉΦ≤ν
ΒΡΫϋΥΤ÷ΒΘ§”Ο―υ±Ψ±ξΉΦ≤ν![]() ΉςΈΣ
ΉςΈΣ![]() ΒΡΙάΦΤ÷ΒΘΜ
ΒΡΙάΦΤ÷ΒΘΜ
Θ®ΔΓΘ©œ÷¥”ΗΟΤϊ≥ΒΙΪΥΨΉν–¬―–ΖΔΒΡ–¬Ρή‘¥Τϊ≥Β÷–»Έ»Γ“ΜΝΨΤϊ≥ΒΘ§«σΥϋΒΡΒΞ¥ΈΉν¥σ–χΚΫάο≥Χ«ΓΚΟ‘Ύ200«ßΟΉΒΫ350«ßΟΉ÷°ΦδΒΡΗ≈¬ ΘΜ
Θ®ΔΔΘ©¥”ΗΟΤϊ≥ΒΙΪΥΨΉν–¬―–ΖΔΒΡ–¬Ρή‘¥Τϊ≥Β÷–ΥφΜζ≥ι»Γ10ΝΨΘ§…η’β10ΝΨΤϊ≥Β÷–ΒΞ¥ΈΉν¥σ–χΚΫάο≥Χ«ΓΚΟ‘Ύ200«ßΟΉΒΫ350«ßΟΉ÷°ΦδΒΡ ΐΝΩΈΣ![]() Θ§«σ
Θ§«σ![]() ΘΜ
ΘΜ
Θ®3Θ©Ρ≥Τϊ≥Βœζ έΙΪΥΨΈΣΆΤΙψ¥ΥΩν–¬Ρή‘¥Τϊ≥ΒΘ§œ÷Οφœρ“βœρΩΆΜßΆΤ≥ωΓΑΆφ”ΈœΖΘ§ΥΆ¥σΫ±Γ±ΜνΕ·Θ§ΩΆΜßΩ…ΗυΨί≈Ή÷ά”≤±“ΒΡΫαΙϊΘ§≤ΌΩΊΈΔ–Ά“ΘΩΊ≥Β‘ΎΖΫΗώΆΦ…œ––ΫχΘ§»τ“ΘΩΊ≥ΒΉν÷’ΆΘ‘ΎΓΑ Λάϊ¥σ±Ψ”ΣΓ±Θ§‘ρΩ…ΜώΒΟΙΚ≥Β”≈Μί»·Θ°“―÷Σ”≤±“≥ωœ÷’ΐΓΔΖ¥ΟφΒΡΗ≈¬ ΕΦ «![]() Θ§ΖΫΗώΆΦ…œ±ξ”–ΒΎ0ΗώΓΔΒΎ1ΗώΓΔΒΎ2ΗώΓΔΓ≠ΓΔΒΎ50ΗώΘ°“ΘΩΊ≥ΒΩΣ Φ‘ΎΒΎ0ΗώΘ§ΩΆΜßΟΩ÷ά“Μ¥Έ”≤±“Θ§“ΘΩΊ≥Βœρ«Α“ΤΕ·“Μ¥ΈΘ§»τ÷ά≥ω’ΐΟφΘ§“ΘΩΊ≥Βœρ«Α“ΤΕ·“ΜΗώΘ®¥”
Θ§ΖΫΗώΆΦ…œ±ξ”–ΒΎ0ΗώΓΔΒΎ1ΗώΓΔΒΎ2ΗώΓΔΓ≠ΓΔΒΎ50ΗώΘ°“ΘΩΊ≥ΒΩΣ Φ‘ΎΒΎ0ΗώΘ§ΩΆΜßΟΩ÷ά“Μ¥Έ”≤±“Θ§“ΘΩΊ≥Βœρ«Α“ΤΕ·“Μ¥ΈΘ§»τ÷ά≥ω’ΐΟφΘ§“ΘΩΊ≥Βœρ«Α“ΤΕ·“ΜΗώΘ®¥”![]() ΒΫ
ΒΫ![]() Θ©Θ§»τ÷ά≥ωΖ¥ΟφΘ§“ΘΩΊ≥Βœρ«Α“ΤΕ·ΝΫΗώΘ®¥”
Θ©Θ§»τ÷ά≥ωΖ¥ΟφΘ§“ΘΩΊ≥Βœρ«Α“ΤΕ·ΝΫΗώΘ®¥”![]() ΒΫ
ΒΫ![]() Θ©Θ§÷±ΒΫ“ΘΩΊ≥Β“ΤΒΫΒΎ49ΗώΘ® Λάϊ¥σ±Ψ”ΣΘ©ΜρΒΎ50ΗώΘ® ßΑή¥σ±Ψ”ΣΘ© ±Θ§”ΈœΖΫα χΘ°…η“ΘΩΊ≥Β“ΤΒΫΒΎ
Θ©Θ§÷±ΒΫ“ΘΩΊ≥Β“ΤΒΫΒΎ49ΗώΘ® Λάϊ¥σ±Ψ”ΣΘ©ΜρΒΎ50ΗώΘ® ßΑή¥σ±Ψ”ΣΘ© ±Θ§”ΈœΖΫα χΘ°…η“ΘΩΊ≥Β“ΤΒΫΒΎ![]() ΗώΒΡΗ≈¬ ΈΣ
ΗώΒΡΗ≈¬ ΈΣ![]() Θ§Τδ÷–
Θ§Τδ÷–![]() Θ§ ‘ΥΒΟς
Θ§ ‘ΥΒΟς![]() «Β»±» ΐΝ–Θ§≤ΔΫβ Ά¥ΥΖΫΑΗΡήΖώ≥…ΙΠΈϋ“ΐΙΥΩΆΙΚ¬ρΗΟΩν–¬Ρή‘¥Τϊ≥Β.
«Β»±» ΐΝ–Θ§≤ΔΫβ Ά¥ΥΖΫΑΗΡήΖώ≥…ΙΠΈϋ“ΐΙΥΩΆΙΚ¬ρΗΟΩν–¬Ρή‘¥Τϊ≥Β.
≤ΈΩΦ ΐΨίΘΚ»τΥφΜζ±δΝΩ![]() Ζΰ¥”’ΐΧ§Ζ÷≤Φ
Ζΰ¥”’ΐΧ§Ζ÷≤Φ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§![]() Θ§
Θ§![]() .
.
ΓΨ¥πΑΗΓΩΘ®1Θ©300ΘΜΘ®2Θ©Θ®iΘ©![]() ΘΜΘ®iiΘ©
ΘΜΘ®iiΘ©![]() ΘΜΘ®3Θ©ΦϊΫβΈωΘ§¥ΥΖΫΑΗΡή≥…ΙΠΈϋ“ΐΙΥΩΆΙΚ¬ρΗΟΩν–¬Ρή‘¥Τϊ≥Β.
ΘΜΘ®3Θ©ΦϊΫβΈωΘ§¥ΥΖΫΑΗΡή≥…ΙΠΈϋ“ΐΙΥΩΆΙΚ¬ρΗΟΩν–¬Ρή‘¥Τϊ≥Β.
ΓΨΫβΈωΓΩ
Θ®1Θ©άϊ”ΟΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΒΡΤΫΨυ ΐΒΡΦΤΥψΖΫΖ®Φ¥Ω…ΒΟ≥ω![]() Θ°
Θ°
Θ®2Θ©Θ®ΔΓΘ©”…![]() Θ§
Θ§![]() Θ°άϊ”Ο’ΐΧ§Ζ÷≤ΦΒΡΕ‘≥Τ–‘Ω…ΒΟ
Θ°άϊ”Ο’ΐΧ§Ζ÷≤ΦΒΡΕ‘≥Τ–‘Ω…ΒΟ![]() Θ°
Θ°
Θ®ΔΔΘ©“άΧβ“β”–![]() Θ§‘Όάϊ”ΟΕΰœνΖ÷≤ΦΒΡΤΎΆϊΙΪ ΫΦΤΥψΩ…ΒΟΘΜ
Θ§‘Όάϊ”ΟΕΰœνΖ÷≤ΦΒΡΤΎΆϊΙΪ ΫΦΤΥψΩ…ΒΟΘΜ
Θ®3Θ©“ΘΩΊ≥ΒΩΣ Φ‘ΎΒΎ0 ΗώΈΣ±Ί»Μ ¬ΦΰΘ§![]() Θ°ΒΎ“Μ¥Έ÷ά”≤±“≥ωœ÷’ΐΟφΘ§“ΘΩΊ≥Β“ΤΒΫΒΎ“ΜΗώΘ§ΤδΗ≈¬ ΈΣ
Θ°ΒΎ“Μ¥Έ÷ά”≤±“≥ωœ÷’ΐΟφΘ§“ΘΩΊ≥Β“ΤΒΫΒΎ“ΜΗώΘ§ΤδΗ≈¬ ΈΣ![]() Θ§Φ¥
Θ§Φ¥![]() Θ°“ΘΩΊ≥Β“ΤΒΫΒΎ
Θ°“ΘΩΊ≥Β“ΤΒΫΒΎ![]() ΗώΒΡ«ιΩω «œ¬ΟφΝΫ÷÷Θ§Εχ«“÷Μ”–ΝΫ÷÷ΘΚΔΌ“ΘΩΊ≥Βœ»ΒΫΒΎ
ΗώΒΡ«ιΩω «œ¬ΟφΝΫ÷÷Θ§Εχ«“÷Μ”–ΝΫ÷÷ΘΚΔΌ“ΘΩΊ≥Βœ»ΒΫΒΎ![]() ΗώΘ§”÷÷ά≥ωΖ¥ΟφΘ§ΤδΗ≈¬ ΈΣ
ΗώΘ§”÷÷ά≥ωΖ¥ΟφΘ§ΤδΗ≈¬ ΈΣ![]() Θ°ΔΎ“ΘΩΊ≥Βœ»ΒΫΒΎ
Θ°ΔΎ“ΘΩΊ≥Βœ»ΒΫΒΎ![]() ΗώΘ§”÷÷ά≥ω’ΐΟφΘ§ΤδΗ≈¬ ΈΣ
ΗώΘ§”÷÷ά≥ω’ΐΟφΘ§ΤδΗ≈¬ ΈΣ![]() Θ°Ω…ΒΟΘΚ
Θ°Ω…ΒΟΘΚ![]() Θ°±δ–ΈΈΣ
Θ°±δ–ΈΈΣ![]() Θ°Φ¥Ω…÷ΛΟς
Θ°Φ¥Ω…÷ΛΟς![]() ±Θ§ ΐΝ–
±Θ§ ΐΝ–![]() «Β»±» ΐΝ–Θ§ ΉœνΈΣ
«Β»±» ΐΝ–Θ§ ΉœνΈΣ![]() Θ§ΙΪ±»ΈΣ
Θ§ΙΪ±»ΈΣ![]() ΒΡΒ»±» ΐΝ–Θ°άϊ”Ο
ΒΡΒ»±» ΐΝ–Θ°άϊ”Ο![]() Θ§ΦΑΤδ«σΚΆΙΪ ΫΦ¥Ω…ΒΟ≥ωΘ°Ω…ΒΟΜώ ΛΒΡΗ≈¬
Θ§ΦΑΤδ«σΚΆΙΪ ΫΦ¥Ω…ΒΟ≥ωΘ°Ω…ΒΟΜώ ΛΒΡΗ≈¬ ![]() Θ§ ßΑήΒΡΗ≈¬
Θ§ ßΑήΒΡΗ≈¬ ![]() Θ°ΫχΕχΒΟ≥ωΫα¬έΘ°
Θ°ΫχΕχΒΟ≥ωΫα¬έΘ°
Θ®1Θ©![]()
![]() Θ®«ßΟΉΘ©.
Θ®«ßΟΉΘ©.
Θ®2Θ©Θ®iΘ©”…![]() .
.
![]()
![]() .
.
Θ®ΔΔΘ©“άΧβ“β”–![]() Θ§Υυ“‘
Θ§Υυ“‘![]() .
.
Θ®3Θ©ΒΎ“Μ¥Έ÷ά”≤±“≥ωœ÷’ΐΟφΘ§“ΘΩΊ≥Β“ΤΒΫΒΎ“ΜΗώΘ§ΤδΗ≈¬ ΈΣ![]() Θ§Φ¥
Θ§Φ¥![]() .
.
“ΘΩΊ≥Β“ΤΒΫΒΎ![]() ΗώΒΡ«ιΩω «œ¬ΟφΝΫ÷÷Θ§Εχ«“÷Μ”–ΝΫ÷÷ΘΜ
ΗώΒΡ«ιΩω «œ¬ΟφΝΫ÷÷Θ§Εχ«“÷Μ”–ΝΫ÷÷ΘΜ
ΔΌ“ΘΩΊ≥Βœ»ΒΫΒΎ![]() ΗώΘ§”÷÷ά≥ωΖ¥ΟφΘ§ΤδΗ≈¬ ΈΣ
ΗώΘ§”÷÷ά≥ωΖ¥ΟφΘ§ΤδΗ≈¬ ΈΣ![]() .
.
ΔΎ“ΘΩΊ≥Βœ»ΒΫΒΎ![]() ΗώΘ§”÷÷ά≥ω’ΐΟφΘ§ΤδΗ≈¬ ΈΣ
ΗώΘ§”÷÷ά≥ω’ΐΟφΘ§ΤδΗ≈¬ ΈΣ![]() .
.
![]() Θ§
Θ§![]() .
.
![]() ±Θ§ ΐΝ–
±Θ§ ΐΝ–![]() «Β»±» ΐΝ–Θ§ ΉœνΈΣ
«Β»±» ΐΝ–Θ§ ΉœνΈΣ![]() Θ§ΙΪ±»ΈΣ
Θ§ΙΪ±»ΈΣ![]() ΒΡΒ»±» ΐΝ–Θ°
ΒΡΒ»±» ΐΝ–Θ°
![]() Θ§
Θ§ Θ§
Θ§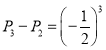 Θ§Γ≠Θ§
Θ§Γ≠Θ§ .
.
![]()
![]()
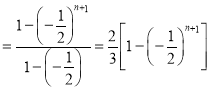
![]() .
.
ΓύΜώ ΛΒΡΗ≈¬  Θ§
Θ§
ßΑήΒΡΗ≈¬ 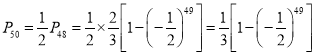 .
.
 .
.
ΓύΜώ ΛΒΡΗ≈¬ ¥σ.
Γύ¥ΥΖΫΑΗΡή≥…ΙΠΈϋ“ΐΙΥΩΆΙΚ¬ρΗΟΩν–¬Ρή‘¥Τϊ≥ΒΘ°


 Οϊ–ΘΝΣΟΥΩλά÷ΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΝΣΟΥΩλά÷ΩΈΧΟœΒΝ–¥πΑΗ ΜΤΗ‘¥¥”≈ΨμœΒΝ–¥πΑΗ
ΜΤΗ‘¥¥”≈ΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΥΡάβΉΕP©¹ABCD÷–Θ§ΒΉΟφABCDΈΣΝβ–ΈΘ§PAΓΆΒΉΟφABCDΘ§ΓœBADΘΫ60ΓψΘ§AB=PAΘΫ4Θ§E «PAΒΡ÷–ΒψΘ§ACΘ§BDΫΜ”ΎΒψO.
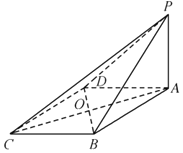
Θ®1Θ©«σ÷ΛΘΚOEΓΈΤΫΟφPBCΘΜ
Θ®2Θ©«σ»ΐάβΉΕE©¹PBDΒΡΧεΜΐ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ°
Θ°
Θ®1Θ©Β±![]() ±Θ§«σ
±Θ§«σ![]() ‘Ύ
‘Ύ![]() …œΒΡΉν–Γ÷ΒΘΜ
…œΒΡΉν–Γ÷ΒΘΜ
Θ®2Θ©»τ÷±œΏ![]() «Κ· ΐ
«Κ· ΐ![]() ΒΡ«–œΏΖΫ≥ΧΘ§«σ Β ΐ
ΒΡ«–œΏΖΫ≥ΧΘ§«σ Β ΐ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®3Θ©»τ![]() Θ§÷ΛΟςΘΚΕ‘»Έ“β Β ΐ
Θ§÷ΛΟςΘΚΕ‘»Έ“β Β ΐ![]() Θ§
Θ§![]() Κψ≥…ΝΔΘ°
Κψ≥…ΝΔΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ –ΜΖ±Θ≤ΩΟ≈Ε‘ΗΟ – –ΟώΫχ––ΝΥ“Μ¥Έά§ΜχΖ÷άύ÷Σ ΕΒΡΆχ¬γΈ ΨμΒς≤ιΘ§ΟΩΈΜ –ΟώΫω”–“Μ¥Έ≤ΈΦ”ΜζΜαΘ§Ά®ΙΐΥφΜζ≥ι―υΘ§ΒΟΒΫ≤Έ”κΈ ΨμΒς≤ιΒΡ100»ΥΒΡΒΟΖ÷Θ®¬ζΖ÷ΘΚ100Ζ÷Θ© ΐΨίΘ§Ά≥ΦΤΫαΙϊ»γ±μΥυ ΨΘΚ
Ήι±π |
|
|
|
|
|
|
Ρ– | 2 | 3 | 5 | 15 | 18 | 12 |
š | 0 | 5 | 10 | 10 | 7 | 13 |
(1)»τΙφΕ®Έ ΨμΒΟΖ÷≤ΜΒΆ”Ύ70Ζ÷ΒΡ –Οώ≥ΤΈΣΓΑΜΖ±ΘΙΊΉΔ’ΏΓ±Θ§«κΆξ≥…¥πΧβΩ®÷–ΒΡ![]() Ν–ΝΣ±μΘ§≤Δ≈–ΕœΡήΖώ‘ΎΖΗ¥μΈσΗ≈¬ ≤Μ≥§Ιΐ0.05ΒΡ«ΑΧαœ¬Θ§»œΈΣ «ΖώΈΣΓΑΜΖ±ΘΙΊΉΔ’ΏΓ±”κ–‘±π”–ΙΊΘΩ
Ν–ΝΣ±μΘ§≤Δ≈–ΕœΡήΖώ‘ΎΖΗ¥μΈσΗ≈¬ ≤Μ≥§Ιΐ0.05ΒΡ«ΑΧαœ¬Θ§»œΈΣ «ΖώΈΣΓΑΜΖ±ΘΙΊΉΔ’ΏΓ±”κ–‘±π”–ΙΊΘΩ
(2)»τΈ ΨμΒΟΖ÷≤ΜΒΆ”Ύ80Ζ÷ΒΡ»Υ≥ΤΈΣΓΑΜΖ±Θ¥ο»ΥΓ±Θ° ”ΤΒ¬ ΈΣΗ≈¬ Θ°
ΔΌ‘ΎΈ“ –Υυ”–ΓΑΜΖ±Θ¥ο»ΥΓ±÷–Θ§ΥφΜζ≥ι»Γ3»ΥΘ§«σ≥ι»ΓΒΡ3»Υ÷–Θ§Φ»”–Ρ–ΓΑΜΖ±Θ¥ο»ΥΓ±”÷”–≈°ΓΑΜΖ±Θ¥ο»ΥΓ±ΒΡΗ≈¬ ΘΜ
ΔΎΈΣΝΥΙΡάχ –ΟώΙΊΉΔΜΖ±ΘΘ§’κΕ‘¥Υ¥ΈΒΡΒς≤ι÷ΤΕ®ΝΥ»γœ¬Ϋ±άχΖΫΑΗΘΚΓΑΜΖ±Θ¥ο»ΥΓ±ΜώΒΟΝΫ¥Έ≥ιΫ±ΜνΕ·ΘΜΤδΥϊ≤Έ”κΒΡ –ΟώΜώΒΟ“Μ¥Έ≥ιΫ±ΜνΕ·Θ°ΟΩ¥Έ≥ιΫ±ΜώΒΟΚλΑϋΒΡΫπΕνΚΆΕ‘”ΠΒΡΗ≈¬ .»γœ¬±μΘΚ
ΚλΑϋΫπΕνΘ®ΒΞΈΜΘΚ‘ΣΘ© | 10 | 20 |
Η≈¬ |
|
|
œ÷Ρ≥ –Οώ“Σ≤ΈΦ”¥Υ¥ΈΈ ΨμΒς≤ιΘ§Φ«![]() Θ®ΒΞΈΜΘΚ‘ΣΘ©ΈΣΗΟ –Οώ≤ΈΦ”ΦδΨμΒς≤ιΜώΒΟΒΡΚλΑϋΫπΕνΘ§«σ
Θ®ΒΞΈΜΘΚ‘ΣΘ©ΈΣΗΟ –Οώ≤ΈΦ”ΦδΨμΒς≤ιΜώΒΟΒΡΚλΑϋΫπΕνΘ§«σ![]() ΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊΘ°
ΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊΘ°
ΗΫ±μΦΑΙΪ ΫΘΚ![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() ‘Ύ
‘Ύ![]() ”κ
”κ![]() ±ΕΦ»ΓΒΟΦΪ÷ΒΘ°
±ΕΦ»ΓΒΟΦΪ÷ΒΘ°
Θ®1Θ©«σ![]() ΒΡ÷Β”κΚ· ΐ
ΒΡ÷Β”κΚ· ΐ![]() ΒΡΒΞΒς«χΦδΘΜ
ΒΡΒΞΒς«χΦδΘΜ
Θ®2Θ©»τΕ‘![]() ,≤ΜΒ» Ϋ
,≤ΜΒ» Ϋ![]() Κψ≥…ΝΔΘ§«σ
Κψ≥…ΝΔΘ§«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΒΡΦΗΚΈΧε![]() ÷–Θ§ΒΉΟφ
÷–Θ§ΒΉΟφ![]() ΈΣΝβ–ΈΘ§
ΈΣΝβ–ΈΘ§ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() ”κ
”κ![]() œύΫΜ”Ύ
œύΫΜ”Ύ![]() ΒψΘ§ΥΡ±Ώ–Έ
ΒψΘ§ΥΡ±Ώ–Έ![]() ΈΣ÷±Ϋ«Χί–ΈΘ§
ΈΣ÷±Ϋ«Χί–ΈΘ§ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ§ΤΫΟφ
Θ§ΤΫΟφ![]() ΒΉΟφ
ΒΉΟφ![]() .
.

Θ®1Θ©÷ΛΟςΘΚΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©«σΕΰΟφΫ«![]() ΒΡ”ύœ“÷Β.
ΒΡ”ύœ“÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΥΡάβΉΕ![]() ÷–Θ§
÷–Θ§![]() Οφ
Οφ![]() Θ§ΒΉΟφ
Θ§ΒΉΟφ![]() ΈΣΝβ–ΈΘ§«“”–
ΈΣΝβ–ΈΘ§«“”–![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ΈΣ
ΈΣ![]() ÷–ΒψΘ°
÷–ΒψΘ°
Θ®1Θ©÷ΛΟςΘΚ![]() Οφ
Οφ![]() ΘΜ
ΘΜ
Θ®2Θ©«σΕΰΟφΫ«![]() ΒΡΤΫΟφΫ«ΒΡ”ύœ“÷ΒΘ°
ΒΡΤΫΟφΫ«ΒΡ”ύœ“÷ΒΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΡάβΉΕ![]() ÷–Θ§ΥΡ±Ώ–Έ
÷–Θ§ΥΡ±Ώ–Έ![]() «ΨΊ–ΈΘ§
«ΨΊ–ΈΘ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ΈΣ’ΐ»ΐΫ«–ΈΘ§«“ΤΫΟφ
ΈΣ’ΐ»ΐΫ«–ΈΘ§«“ΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§
Θ§![]() ΓΔ
ΓΔ![]() Ζ÷±πΈΣ
Ζ÷±πΈΣ![]() ΓΔ
ΓΔ![]() ΒΡ÷–Βψ.
ΒΡ÷–Βψ.

Θ®1Θ©÷ΛΟςΘΚ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©«σΦΗΚΈΧε![]() ΒΡΧεΜΐ.
ΒΡΧεΜΐ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]()
Θ®1Θ©»τΚ· ΐ![]() ‘Ύ
‘Ύ![]() …œΒίΦθΘ§‘Ύ
…œΒίΦθΘ§‘Ύ![]() …œΒί‘ωΘ§«σ Β ΐ
…œΒί‘ωΘ§«σ Β ΐ![]() ΒΡ÷Β.
ΒΡ÷Β.
Θ®2Θ©»τΚ· ΐ![]() ‘ΎΕ®“ε”ρ…œ≤ΜΒΞΒςΘ§«σ Β ΐ
‘ΎΕ®“ε”ρ…œ≤ΜΒΞΒςΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
Θ®3Θ©»τΖΫ≥Χ![]() ”–ΝΫΗω≤ΜΒ» Β ΐΗυ
”–ΝΫΗω≤ΜΒ» Β ΐΗυ![]() Θ§«σ Β ΐ
Θ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΘ§≤Δ÷ΛΟς
ΒΡ»Γ÷ΒΖΕΈßΘ§≤Δ÷ΛΟς![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com