练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．对变量X与Y的卡方统计量Χ2的值，说法正确的是（　　）
    A．Χ2越大，“X与Y有关系”可信程度越小
    B．Χ2越小，“X与Y有关系”可信程度越小
    C．Χ2越接近0，“X与Y无关”程度越小
    D．Χ2越大，“X与Y无关”程度越大

    分析 根据相关指数Χ2越小，“X与Y有关系”可信程度越小，可得答案．

    解答 解：根据相关指数Χ2越小，“X与Y有关系”可信程度越小，
    判定B正确．
    故选：B．

    点评 本题考查了独立性检验的基础知识，熟练掌握相关指数Χ2的观测值的含义是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    19．某单位决定建造一批简易房（房型为长方体状，房高2.5米），前后墙用2.5米高的彩色钢板，两侧用2.5米高的复合钢板，两种钢板的价格都用长度来计算（即：钢板的高均为2.5米，用钢板的长度乘以单价就是这块钢板的价格），每米单价：彩色钢板为450元，复合钢板为200元．房顶用其它材料建造，每平方米材料费为200元．每套房材料费控制在32000元以内．
    （1）设房前面墙的长为x，两侧墙的长为y，所用材料费为p，试用x，y表示p；
    （2）在材料费的控制下简易房面积S的最大值是多少？并指出前面墙的长度x应为多少米时S最大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．函数f（x），x∈R满足如下性质：①f（x）+f（-x）=0；②f（$\frac{3}{4}$+x）=f（$\frac{3}{4}$-x），若f（1）=-$\frac{\sqrt{5}}{5}$，f（2）=sinα（α∈（0，$\frac{π}{2}$）），则sin（$\frac{π}{4}$+α）=（　　）
    A．0B．$\frac{\sqrt{10}}{10}$C．$\frac{2\sqrt{10}}{10}$D．$\frac{3\sqrt{10}}{10}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

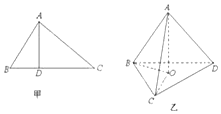    7．如图甲，在△ABC中，AB⊥AC，AD⊥BC，D为．垂足，则AB2=BD•BC，该结论称为射影定理．如图乙，在三棱锥A-BCD中，AD⊥平面ABC，AO⊥平面BCD，O为垂足，且O在△BCD内，类比射影定理，探究S△ABC、S△BCO、S△BCD这三者之间满足的关是S△ABC2=S△BCO•S△BCD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．（1）已知O是△ABC内任意一点，连接AO，BO，CO并延长交对边于A′，B′，C′，则$\frac{{O{A^'}}}{{A{A^'}}}+\frac{{O{B^'}}}{{B{B^'}}}+\frac{{O{C^'}}}{{C{C^'}}}=1$，这是一道平面几何题，其证明常采用“面积法”：$\frac{{O{A^'}}}{{A{A^'}}}+\frac{{O{B^'}}}{{B{B^'}}}+\frac{{O{C^'}}}{{C{C^'}}}=\frac{{{S_{△OBC}}}}{{{S_{△ABC}}}}+\frac{{{S_{△OCA}}}}{{{S_{△ABC}}}}+\frac{{{S_{△OAB}}}}{{{S_{△ABC}}}}=1$．
    请运用类比思想，对于空间中的四面体A-BCD，存在什么类似的结论？并用体积法证明．
    （2）已知0＜x＜2，0＜y＜2，0＜z＜2，求证：x（2-y），y（2-z），z（2-x）不都大于1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

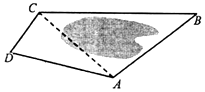    4．如图为了测量A，C两点间的距离，选取同一平面上B，D两点，测出四边形ABCD的各边的AB=5，BC=8，CD=3，DA=5长度（单位：km）：，如图所示，若A、B、C、D四点共圆．
    求：线段AC的长和△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

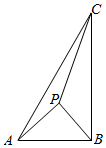    11．如图，在△ABC中，∠ABC=90°，AB=1，BC=$\sqrt{3}$，P为△ABC内一点，∠APB=90°．
    （1）若PA=$\frac{{\sqrt{3}}}{2}$，求PB；
    （2）若∠BPC=120°，求tan∠PCB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知m∈R，复数z=（1+i）m2-（8+5i）m+15-14i．
    （Ⅰ）若复数z为纯虚数，求实数m的值；
    （Ⅱ）若在复平面内复数z表示的点在第四象限，求实数m的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．若数列{an}是正项数列，且$\sqrt{a_1}+\sqrt{a_2}+\sqrt{a_3}+…+\sqrt{a_n}={n^2}+n$，则$\frac{a_1}{1}+\frac{a_2}{2}+…+\frac{a_n}{n}$=2n2+2n．

    查看答案和解析>>

    同步练习册答案